ОСНОВЫ ТЕОРИИ ГРАФОВ

Теория графов – это раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами.

Графы представляют собой наиболее абстрактную струк­туру, с которой приходится сталкиваться в курсах математиче­ской логики, дискретной математики, теории сетей связи. Любая система, предполагающая наличие дискретных состояний или узлов и переходов между ними, может быть описана графом.

Граф – это совокупность вершин (узлов) и связывающих их ребер (ветвей). Графы отображаются на плоскости набором точек и соединяющих их линий или векторов. При этом ветви могут отображаться и кривыми линиями, а их длина не играет никакой роли. Граф называется ориентированным (или оргра­фом),если некоторые ребра имеют определенное направление, Это означает, что в орграфе некоторая вершина может быть со­единена с другой вершиной, а обратного соединения нет. Ребра орграфа называются дугами.

Смежные вершины графа - вершины, инцидентные одно­му я тому же ребру (принадлежащие одному ребру). Ребро гра­фа определяется парой вершин. Два ребра, инцидентные одной и той же вершине (у которых есть общая вершина), также назы­ваются смежными (или соседними).

Математически граф G можно описать упорядоченной парой множеств N и А:

G = (N , А),

где N – непустое множество, называемое множеством вершин; А – множество ребер, отражающее отношение между вершинами.

Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным;граф,в котором направление линий принципиально(линии являются дугами) называется ориентированным.

Часть графа – граф, образованный из исходного удалени­ем некоторых вершин и ребер. Подграфом называется часть графа,образованная подмножествомвершин вместе со своими ребрами (дугами), соединяющими вершины из этого множества. Суграф – часть графа, образованная удалением из исходного графа некоторых ребер.

Петлей называется ребро, концевые точки которого сов­падают. Степенью (валентностью) вершины называется число инцидентных ей ребер. Кратностью пары вершин называется число соединяющих их ребер.

Ветви дерева – ребра графа, вошедшие в дерево. Хорды – ребра графа, не вошедшие в дерево.

Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) – инцидентным соответствующим вершинам.

Графы равны, если множества вершин и инцидентных им ребер совпадают.

Графы, отличающиеся только нумерацией вершин и ребер, называются изоморфными.

Ребра, инцидентные одной паре вершин, называются параллельными или кратными.

Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.

Граф с кратными ребрами называется мультиграфом.

Граф, содержащий петли (т.е. некоторая вершина соединена сама с собой ребром) и кратные ребра, называется псевдографом.

Конечный граф–число вершин и ребер конечно.

Полный граф–граф без петель и кратных ребер,каждая пара вершинсоединена ребром.

Граф является связным, если можно указать маршрут, ох­ватывающий все вершины.

Дерево графа - связный граф, не имеющий циклов.

Фундаментальное дерево (остов) - связный граф, не имею­щий циклов.

Примеры графа, подграфа, суграфа и фундаментального дерева представлены на рис. 1.

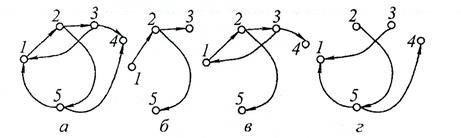
Рис. 5.1 Структуры: а – граф; б – подграф; в – суграф; г – фундаментальное дерево

Маршрут в графе–это последовательность ребер,в которых каждыедва соседних ребра имеют общую вершину. Причем одно и то же ребро может встречаться в маршруте несколько раз. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Цепью называется множество ребер,которые можно расположить так,что конец одного ребра является началом другого. То есть цепь – это маршрут в неографе, в котором все ребра разные. Замкнутая цепь также называется циклом.

Путем называется последовательность дуг(в ориентированном графе),такая, что конец одной дуги является началом другой дуги. Простой путь – путь, в котором ни одна дуга не встречается дважды. Элементарный путь – путь, в котором ни одна вершина не встречается дважды в графе.

Контур –это цикл без повторения вершин,за исключением первойвершины, совпадающей с последней. Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если последние заданы).

Последовательности вершин (рис. 5.1): 1–2–3–4–2–5 не простой путь, маршрут; последовательности 1–2–3–4–7–5 и 1–2–5 – простые пути; 1–2–3–4–2–5–6–1 – это цикл (но не контур); 1–2–5–6–1 – это контур.

Если имеется некоторый маршрут из вершины t в вершину s, заданный графа, называется гамильтоновой цепью (соответственно – циклом, путем, контуром).

Простая цепь (цикл, путь, контур), содержащая все ребра (дуги) графа, называется эйлеровой цепью (соответственно – циклом, путем, контуром).

Граф называется связным, если любые две его вершины можно соединить маршрутом (цепью или путем).

Ребро, при удалении которого граф перестает быть связным, иногда называют мостом или перешейком.

Если граф не является связным, то его можно разбить на связные подграфы, называемые компонентами. Связностью графа называется минимальное число ребер, после удаления которых, граф становится несвязным. Для ориентированных графов: если любые две вершины графа можно соединить путем, то граф называется сильно связным.

Связный граф, в котором существует эйлеров цикл, называется эйлеровым графом.

Степень вершины –это число ребер,входящих в эту вершину.Вершинаназывается висячей, если ее степень равна единице.

Матрицы графов

Важным вопросом, особенно для приложений теории графов, является определение возможных способов представления графов. Самый простой способ – полное перечисление множеств X и V. Однако в этом случае выявление у графа различных характеристик и свойств будет крайне затруднительным. Граф можно представить в виде некоторого графического изображения и визуально определить некоторые свойства и характеристики заданного графа. Однако при наличии большого числа ребер и вершин этот способ также мало пригоден. Лучше всего представить граф в числовом виде, в виде матрицы.

Матрица смежности.Это квадратная матрица А(G) порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности a_ij равен единице, если эти вершины связаны s ребрами, то а_ij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.

Матрица инцидентности –это матрица B(G) размера n - m,где n – число вершин, а m – число ребер графа, при этом ее элементы k_ij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер.

Для ориентированного графа матрица достижимости – это квадратная матрица C(G) размера порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина j достижима из вершины i одной дугой, то элемент матрицы достижимости с_ij равен 1, если эти вершины связаны s дугами, то а_ij= s.