Математические модели решений организационно-экономических задач производства

В области машиностроения наиболее часто встречающим­ся приложением алгоритмов и теоретических методов, рассмат­риваемых теорией графов, является решение задач о потоках в сетях (сетевые модели).

Изучение сетевых моделей началось в 40-х годах XX в. в связи с транспортными задачами, т.е. задачами о прикрепле­нии поставщиков к потребителям, минимизирующем суммар­ные расходы по перевозке.

Разновидностью таких задач являются часто встречаю­щиеся на практике задачи максимизации потока некоего про­дукта между двумя заданными узлами сети при условии, что поток вдоль каждой дуга ограничен. В этом разделе формули­руются основные принципы и излагается метод решения ука­занного класса сетевых задач.

Решение задачи о максимальном потоке

Задача максимального потока формулируется следующим образом.

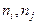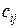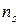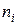Пусть каждой дуге ( ) сети G = (N, А) поставлено в со­ответствие некоторое неотрицательное вещественное число , называемое пропускной способностью дуги. Выделим на сети два узла: и ,которые назовем источником и стоком соот­ветственно. Тогда потоком величины F из 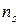в 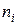называется функция х, отображающая А на множество неотрицательных вещественных чисел и удовлетворяющая условиям

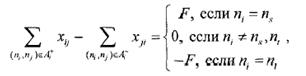
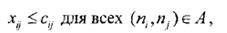
где А_i* - множество дуг с начальным узлом 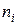, а A_i^- - множест­во дуг с конечным узлом 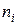Величина 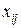, называется потоком по дуге ( ).

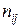Суммарный поток из каж­дого промежуточного узла равен 0, а суммарный поток в сток равен F.Из уравнения следует, что поток по каждой дуге не превышает ее пропускной способности.

Максимальным потоком из 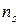в 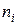назовем такую функцию х,удовлетворяющую представленным уравнениям, для которой величина F макси­мальна.

Пример потока в сети дан на рис., на котором первое число, поставленное в соответствие каждой дуге – ее пропускная способность, а второе – поток по дуге.

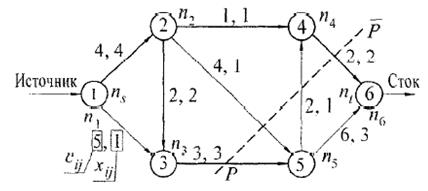
Рис 5.2 Поток в сети (величиной F=5)

Физически поток можно представить как количество условного «груза», перевозимого из вершины с номером i в вершину с номером j , а суммарный поток F – как количество груза, перевозимого из источника в сток.

Транспортная задача

Рассматривается случай нескольких истоков и стоков с ограничением на их мощности.

Пусть имеется т сталепрокатных заводов х₁, х₂, …, х_т, и каждый из заводов х_i может производить с(х_j) тонн проката в неделю. Стоимость перевозки одной тонны из х_i в y_j равна .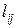

Сколько проката надо производить на каждом заводе и куда его направлять, чтобы с минимальными расходами удовлетворить потребности всех металлообрабатывающих предприятий?

В терминах сетевой модели проблема может быть сформулирована как задача нахождения максимального потока минимальной стоимости в сети, где первые числа указывают пропускную способность, а вторые – стоимость каждой дуги.

Вопросы для самопроверки

1. Как изображается граф?

2. Что определяют понятия: ребро, дуга, путь?

3. Как изображается вершина графа, ребро графа?

4. Как называются графы, отличающиеся только номерами вершин и ребер?

5. Какой граф называется мультиграфом?

6. Какой маршрут в графе называют циклом?

7. Какой маршрут в графе называют цепью?

8. Как называют вершины графа, которые не принадлежат ни одному ребру?

9. Как называют связной граф без циклов?

10. Изобразите полный граф и псевдограф.