Решение задачи графическим способом
Для определения режимов резания для двух элементов s и n широко применяется метод линейного программирования, общая задача которого состоит в определении неотрицательных значений переменных, удовлетворяющих системе ограничений в виде линейных равенств и неравенств и обеспечивающих наибольшее и наименьшее значение некоторой линейной функции – критерия оптимальности. Таким образом, первая задача – приведение всех технических ограничений и оценочной функции к линейному виду.
Имеем скорость резания для различных видов обработки
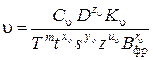
где 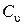 – постоянный коэффициент, характеризующий нормативные условия обработки; D – диаметр обрабатываемой детали;
– постоянный коэффициент, характеризующий нормативные условия обработки; D – диаметр обрабатываемой детали; 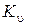 – поправочный коэффициент, учитывающий качество обрабатываемого материала, состояние поверхности заготовки и характеристику режущего инструмента; Т – принятая стойкость инструмента, мин; m – показатель относительной стойкости; t – глубина резания, мм; s – подача, мм/об; z – число зубьев режущего инструмента;
– поправочный коэффициент, учитывающий качество обрабатываемого материала, состояние поверхности заготовки и характеристику режущего инструмента; Т – принятая стойкость инструмента, мин; m – показатель относительной стойкости; t – глубина резания, мм; s – подача, мм/об; z – число зубьев режущего инструмента; 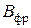 – ширина фрезерования;
– ширина фрезерования; 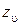 ,
, 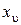 ,
, 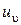 ,
, 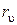 – показатели степеней.
– показатели степеней.
Рассмотрим приведение к линейному виду для технического ограничения по режущим возможностям инструмента методом логарифмирования:
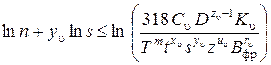 .
.
Введем обозначения
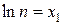 ,
,
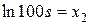 ,
,
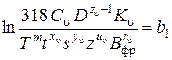 ,
,
подставим их в неравенство и получим
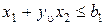 .
.
Аналогично могут быть получены в линейном виде зависимости и для других ограничений.
Математическую модель процесса резания можно изобразить в графическом виде. При этом каждое техническое ограничение представляется граничной прямой, которая определяет полуплоскость, где возможно существование решений системы неравенств. Граничные переменные, пересекаясь, образуют многоугольник АВСDEF, внутри которого любая точка удовлетворяет всем без исключения неравенствам системы, поэтому этот многоугольник называют многоугольником решений.
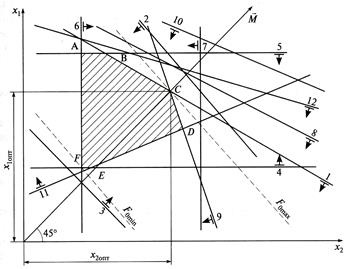
Рис. 7.1 Графическое изображение математической модели процесса резания
Теория линейного программирования показывает, что экстремальное значение оценочной функции (при выпуклом многоугольнике решений) обеспечивается для 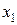 и
и 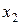 , находящихся в точке, лежащей на одной из граничных прямых или их пересечении. Поэтому задача отыскания оптимальных значений
, находящихся в точке, лежащей на одной из граничных прямых или их пересечении. Поэтому задача отыскания оптимальных значений 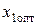 и
и 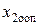 сводится к последовательному вычислению координат всех возможных точек пересечения граничных прямых, а затем к определению для них максимального значения суммы
сводится к последовательному вычислению координат всех возможных точек пересечения граничных прямых, а затем к определению для них максимального значения суммы 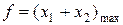 .
.
Дата добавления: 2021-01-11; просмотров: 493;











