Непрямой адаптивный нечеткий контроллер
Уравнения движения некоторого класса нелинейных динамических объектов в непрерывной области можно представить в канонической (аффинной) форме
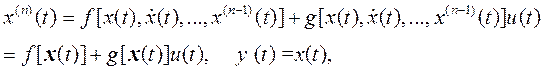 (1)
(1)
где f и g неизвестные нелинейные функции с предположением g>0 , u и y скалярные вход (управление) и выход ОУ соответственно.
Цель управления принудить вектор состояния 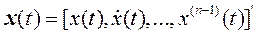 отслеживать конкретную желаемую траекторию
отслеживать конкретную желаемую траекторию 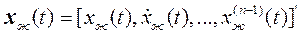 , другими словами, заставить y(t)следить за изменениями желаемого сигнала
, другими словами, заставить y(t)следить за изменениями желаемого сигнала 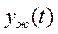 =
=  . Если мы определим векторную ошибку слежения как
. Если мы определим векторную ошибку слежения как 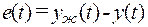 , то целью управления можно считать проектирование закона управления, который обеспечивает
, то целью управления можно считать проектирование закона управления, который обеспечивает  при
при 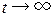 . Уравнение (1) описывает объект, который можно преобразовать в линейный объект, используя линеаризацию обратной связью, если
. Уравнение (1) описывает объект, который можно преобразовать в линейный объект, используя линеаризацию обратной связью, если 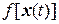 и
и 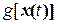 точно известная функция. Конкретно следующий закон управления
точно известная функция. Конкретно следующий закон управления
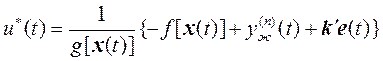 (2)
(2)
преобразует с учетом 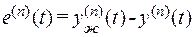 и
и 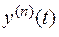 =
= 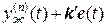 исходное нелинейное уравнение (1) в линейное уравнение для ошибки
исходное нелинейное уравнение (1) в линейное уравнение для ошибки
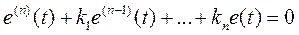 , (3)
, (3)
где 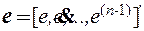 и
и 
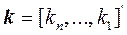 представляет собой соответствующим образом выбранный вектор, при котором все корни характеристического уравнения
представляет собой соответствующим образом выбранный вектор, при котором все корни характеристического уравнения 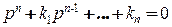 являются левыми, так что этот вектор обеспечивает
являются левыми, так что этот вектор обеспечивает  при
при 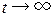 , т. е. выход объекта y сходится асимптотически к идеальному выходу yж.
, т. е. выход объекта y сходится асимптотически к идеальному выходу yж.
Так как функции f и g неизвестны, то интуитивным кандидатом на роль u в (2) должно быть управление
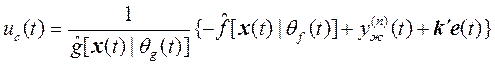 . (4)
. (4)
Здесь 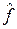 и
и 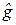 являются параметризованными соответственно функциями
являются параметризованными соответственно функциями 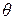 f и
f и 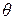 g, реализуемыми адаптивным устройством, которое обладает достаточно хорошими свойствами, чтобы аппроксимировать
g, реализуемыми адаптивным устройством, которое обладает достаточно хорошими свойствами, чтобы аппроксимировать 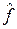 и
и 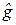 . Разумно получить оценки
. Разумно получить оценки 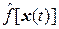 =
= 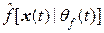 ,
, 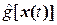 =
= 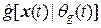 соответственно для неизвестных функций
соответственно для неизвестных функций 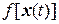 и
и 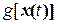 , используя нечеткую систему, описываемую правилами:
, используя нечеткую систему, описываемую правилами:
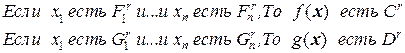 (5)
(5)
Типично неизвестные векторы параметров 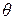 f и
f и 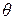 g являются центрами нечетких множеств выхода
g являются центрами нечетких множеств выхода 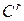 и
и 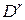 в правилах (5). Используя синглтонную фаззификацию, конъюнкцию и импликацию в виде алгебраического произведения, дефаззификацию в форме центра тяжести, и следуя процедуре, изложенной в лекции 12, оценки можно записать в следующем виде
в правилах (5). Используя синглтонную фаззификацию, конъюнкцию и импликацию в виде алгебраического произведения, дефаззификацию в форме центра тяжести, и следуя процедуре, изложенной в лекции 12, оценки можно записать в следующем виде
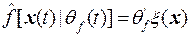 , (6)
, (6)
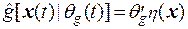 , (7)
, (7)
где 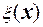 и
и 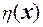 нечеткие базисные функции, определенные соответственно для
нечеткие базисные функции, определенные соответственно для 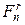 и
и 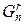 аналогично выражению ().
аналогично выражению ().
Следующий шаг настроить векторы параметров 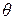 f и
f и 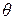 g так, чтобы ошибка слежения (воспроизведения) e и ошибки параметров
g так, чтобы ошибка слежения (воспроизведения) e и ошибки параметров 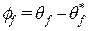 и
и 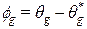 были минимальными. В последних выражениях
были минимальными. В последних выражениях 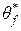 и
и 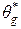 представляют собой оптимальные значения параметров, определяемые как
представляют собой оптимальные значения параметров, определяемые как
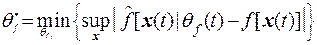 , (8)
, (8)
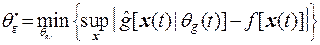 . (9)
. (9)
При этом минимальная ошибка аппроксимации, т.е. ошибка от замены правой части (1) для u(t)=uc (t) на
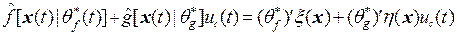 , (10)
, (10)
равна
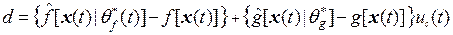 . (11)
. (11)
Выражая из (4)
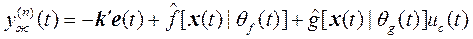 ,
,
с учетом (1) получаем
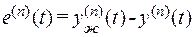 =
= 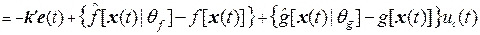
или в матричной форме

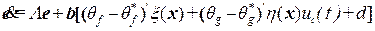 , (12)
, (12)

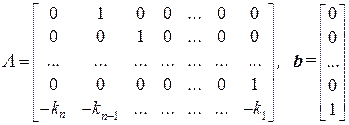 . (13)
. (13)
При этом принято во внимание, что с учетом (6), (7), (10) и (11)
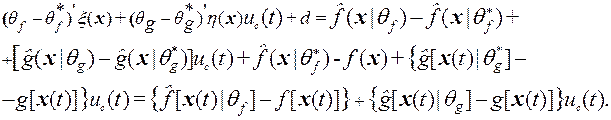
Продолжая рассмотрение задачи минимизации ошибки аппроксимации, воспользуемся методом синтеза Ляпунова и определим следующую функцию Ляпунова
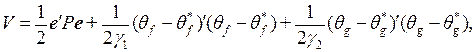 (14)
(14)
где 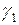 и
и 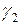 постоянные и P симметричная положительно определенная матрица, удовлетворяющая уравнению Ляпунова
постоянные и P симметричная положительно определенная матрица, удовлетворяющая уравнению Ляпунова
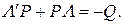
Здесь Q матрица, определяемая проектировщиком системы. Заметим , что решение уравнения всегда существует, т.к все собственные значения матрицы 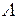 являются левыми в силу выбора коэффициентов
являются левыми в силу выбора коэффициентов 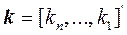 . Производная от функции Ляпунова по времени с учетом (12) определяется следующим выражением
. Производная от функции Ляпунова по времени с учетом (12) определяется следующим выражением
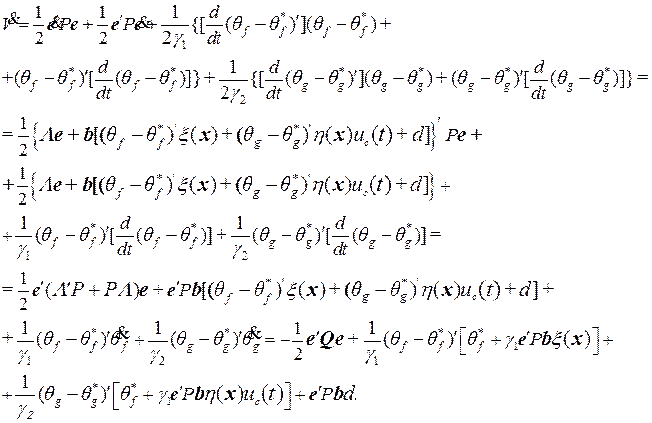
При получении окончательного результата для 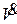 было принято во внимание, что производные по времени от
было принято во внимание, что производные по времени от  и
и  равны нулю, а также то, что транспонирование скалярной величины не изменяет ее выражения.
равны нулю, а также то, что транспонирование скалярной величины не изменяет ее выражения.
Закон адаптации, который минимизирует функцию Ляпунова имеет следующий вид
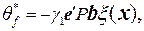
 .
.
Отсюда
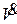 =
= 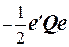 +
+ 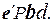
Если d=0, то 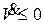 , т.к. Q положительно определенная матрица. Если
, т.к. Q положительно определенная матрица. Если 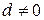 , то следует ожидать, что в соответствие с теоремой об универсальной аппроксимации |d| будет малой величиной. Следовательно, если Q выбрано соответствующим образом, то можно обеспечить выполнение условия
, то следует ожидать, что в соответствие с теоремой об универсальной аппроксимации |d| будет малой величиной. Следовательно, если Q выбрано соответствующим образом, то можно обеспечить выполнение условия 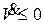 . При V > 0 и
. При V > 0 и 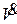 < 0 легко установить, что в соответствии с (14) функции
< 0 легко установить, что в соответствии с (14) функции 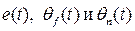 являются ограниченными. Следовательно,
являются ограниченными. Следовательно, 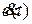 также ограниченная функция в соответствии с (12). Отсюда согласно лемме Барбалата
также ограниченная функция в соответствии с (12). Отсюда согласно лемме Барбалата
 .
.


Используя этот закон управления, получаем замкнутую систему, описываемую уравнением
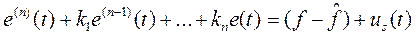 . (5)
. (5)
Дата добавления: 2021-01-11; просмотров: 649;











