Моделирование нелинейных динамических процессов (объектов)

Способность нейронных сетей осуществлять нелинейное преобразование

сигналов может быть использовано для моделирования нелинейных динамических объектов. В этом случае модель находится путем обучения нейронной сети, т.е. путем настройки весов так, чтобы минимизировать ошибку моделирования.

Использование нейронных сетей для моделирования поясним на примере дискретного динамического объекта с одним входом и одним выходом. Предположим, что на вход такого объекта поступает управляющая последовательность u [i] , а на выходе с помощью датчика измеряется управляемая последовательность y[i]. Пусть известно, что дискретная модель объекта является моделью второго порядка. Заметим, что выбор порядка модели относится к проблемам идентификации нелинейных систем, но не является предметом данного курса лекций. Тогда общее описание нейронной динамической модели с тремя входными и одним выходным сигналом можно выразить в форме

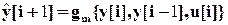. (30)

В этом уравнении 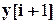обозначает реакцию нелинейного объекта в момент t=(i+1)T, а 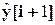- реакцию нейронной динамической модели этого объекта в то же момент времени. Для сравнения линейный аналог этой нейронной модели описывается как

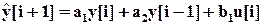(31)

с параметрами a₁, a₂, b₁ , подлежащими оценке, и называется авторегрессионной моделью (ARX-моделью). Разностный сигнал

e[i+1]= -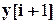

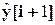
управляет процессом настройки весов нейронной модели.

В случае применения для моделирования объектов нейронная сеть обычно подключается параллельно объекту и использует для предсказания смещенные в сторону запаздывания выходные последовательности объекта так, как это показано на рис. 9.

Рис. 9

При таком подключении реакция сети зависит от входа u[(iT)] , а также

от сигналов d₁[iT] =y[iT] и d₂[iT]= y[(i-1)T], представляющих собой две прошедшие через линии задержки T реализации желаемого сигнала, составляющих ожидаемый выходной вектор сети. В этой ситуации нейронная сеть выполняет функции классической многослойной статической сети.

Для примера рассмотрим моделирование нелинейного динамического

объекта Винера. В нейронной модели этого объекта использовалась сеть с одним скрытым слоем из 25 нейронов. После подбора значений весов тестировалась способность сети к обобщению, для чего на ее вход подавался синусоидальный сигнал. На рис. 10 показаны графики изменения сигнала, полученного на выходе нелинейного объекта (пунктирная линия), и сигнала, имеющего место на выходе нейронной сети.

Рис. 10

Найденная нейронная модель тестируется с помощью свободного запуска (free run»)(рис. 11).

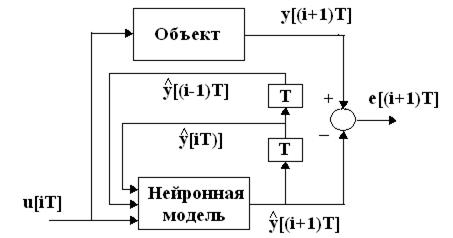
Рис. 11

Термин свободный запуск используется, чтобы подчеркнуть контраст с так называемым предсказанием на один период дискретизации («one-step- ahead prediction») (рис.10). При свободном запуске оценки выходов объекта используются как входы нейронной сети вместо измеренных значений. Таким путем модель может быть использована, чтобы моделировать объект независимо от измеренных настоящего и прошлых значений выхода. Если модель используется для предсказания на несколько периодов дискретизации (на некоторый горизонт), как это необходимо при управлении с предсказанием, свободный запуск представляет собой более дискриминационный тест и более удобен для тестирования модели, чем модель тестирования, опирающаяся на предсказание на один период дискретизации.