Технология инференции (нечеткого логического вывода)
Рассмотрим второй подход для нечеткого логического вывода, который в явном виде не использует отношения.
Упрощенный алгоритм нечеткого логического вывода.Прежде чем описывать механизм инференции (нечеткого логического вывода), используемый при проектировании нечетких контроллеров, снова обратимся к ОМП (обобщенному правилу модус поненс), рассмотренному в первой главе. Мы вновь касаемся этого вопроса, потому что алгоритм инференции при проектировании нечетких контроллеров является упрощенным по сравнению с алгоритмом, с которым вы познакомились в упомянутой главе. Правило ОМП записывается как
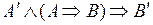 .
.
Лингвистический смысл этого правила заключается в следующем. Пусть высказывания 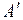 ,
, 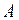 ,
, 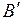 ,
, 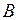 представляют собой четыре лингвистических переменные, каждая из которых может принимать лишь одно значение (один терм), другими словами, каждое из высказываний есть нечеткое множество. Известно из опыта работы или по мнению экспертов, что нечеткое множество
представляют собой четыре лингвистических переменные, каждая из которых может принимать лишь одно значение (один терм), другими словами, каждое из высказываний есть нечеткое множество. Известно из опыта работы или по мнению экспертов, что нечеткое множество 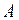 влечет за собой нечеткое множество
влечет за собой нечеткое множество 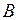 . В результате измерения (наблюдения) установлено, что на самом деле имеет место нечеткое множество
. В результате измерения (наблюдения) установлено, что на самом деле имеет место нечеткое множество 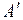 в какой-то степени близкое к множеству
в какой-то степени близкое к множеству 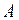 . Тогда согласно правилу ОМП нечеткое множество
. Тогда согласно правилу ОМП нечеткое множество 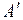 влечет за собой нечеткое множество
влечет за собой нечеткое множество 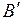 , близкое множеству
, близкое множеству 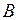 в такой же степени, в какой множество
в такой же степени, в какой множество 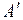 близко к множеству
близко к множеству 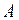 .
.
Степень выполнения условия (скалярная величина) 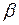 , другими словами, степень истинности высказывания «множество
, другими словами, степень истинности высказывания «множество 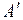 близко множеству
близко множеству 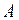 » определяется как максиминная композиция между этими множествами
» определяется как максиминная композиция между этими множествами
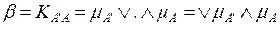 , (2.10)
, (2.10)
причем 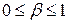 .
.
Здесь 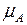 и
и 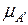 соответственно функции принадлежности (ФП) множеств
соответственно функции принадлежности (ФП) множеств 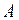 и
и 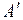 (см. рисунок ниже).
(см. рисунок ниже).
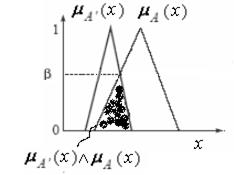
Очевидно, что, если нечеткое множество 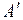 равно нечеткому множеству
равно нечеткому множеству 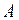 , так что
, так что 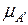 =
= 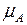 , и функция принадлежности
, и функция принадлежности 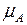 нормализована, то степень истинности
нормализована, то степень истинности 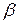 =1.
=1.
В соответствии с ОМП композиция между множествами 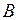 и
и 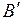 должна быть равна
должна быть равна 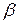 , т.е.
, т.е.
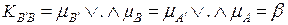 . (2.11)
. (2.11)
Отсюда делаем нечеткий логический вывод о том, что нечеткое множество 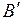 определяется функцией принадлежности
определяется функцией принадлежности
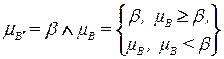 . (2.12)
. (2.12)
Здесь под операцией 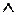 понимается min. Легко показать, что при этом композиция
понимается min. Легко показать, что при этом композиция 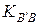 , отражающая степень близости множеств
, отражающая степень близости множеств 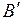 и
и 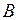 , равна
, равна 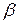 . Действительно, учитывая (2.12) и принимая во внимание, что для множества
. Действительно, учитывая (2.12) и принимая во внимание, что для множества 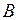 справедливо соотношение
справедливо соотношение
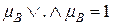 , (2.13)
, (2.13)
получаем
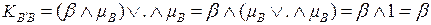 . (2.14)
. (2.14)
Рассмотренный упрощенный метод нечеткого логического вывода разработан Мамдани и носит название максиминной инференции или инференции Мамдани. По сравнению с методом, описанным в разделе 1.4.3 и в соответствии с которым множество 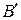 определяется согласно (1.19) как композиция множества
определяется согласно (1.19) как композиция множества 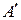 и отношения
и отношения 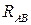
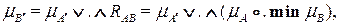
метод Мамдани позволяет избежать вычисления отношения 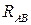 для получения окончательного результата, что является его достоинством, т.к. позволяет обойтись без дискретизации отношения
для получения окончательного результата, что является его достоинством, т.к. позволяет обойтись без дискретизации отношения 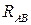 и последующего сохранения в памяти его элементов.
и последующего сохранения в памяти его элементов.
Дадим более строгое доказательство (2.12). Так как операции по определению внешнего и внутреннего произведений в (1.19) осуществляются в различных универсумах (областях), то можно изменить их (операций) порядок:
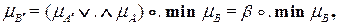
где постоянная
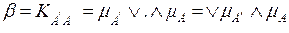
определяется выражением (2.10). В силу постоянства 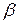 (
( 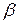 =const) внешнее произведение
=const) внешнее произведение 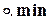 эквивалентно операции
эквивалентно операции 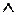 . Отсюда приходим к полученному интуитивно выражению (2.12) для ФП нечеткого множества
. Отсюда приходим к полученному интуитивно выражению (2.12) для ФП нечеткого множества 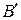 . Как видим, метод Мамдани вытекает из метода, основанного на композиции множества
. Как видим, метод Мамдани вытекает из метода, основанного на композиции множества 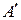 и отношения
и отношения 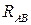 .
.
Дата добавления: 2021-01-11; просмотров: 685;











