Проектирование нечетких контроллеров (метод Мамдани)

Перейдем теперь к проектированию нечетких контроллеров, используя рассмотренный алгоритм нечеткого вывода (формулы (2.10), (2.12)).

1. Нечеткий контроллер с одним входом и одним выходом

Пусть нечеткое правило, установленное с помощью экспертов, гласит:

Если ошибка e есть 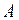, то управление u есть 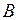. (2.15)

Это правило называется лингвистической моделью нечеткого контроллера.

В результате измерений получено, что ошибка принимает другое лингвистическое значение, нечеткое множество 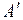. Делаем логический вывод: управление есть 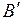, в такой же степени близкое множеству 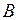, в какой степени 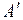близко к .

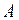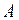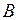Пусть ФП термов и определены и имеют вид 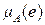и 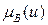(рис. 2.7,а). Известна ФП 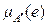для множества 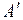. Заметим, что множества 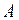и 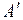заданы на одном универсуме. При этом степень истинности утверждения «нечеткое множество 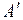близко к множеству 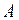» определяется композицией (шаг 1 алгоритма нечеткого логического вывода)

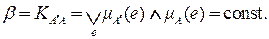(2.16)

Отсюда нечеткий логический вывод (заключение) приводит к ФП (шаг 2 алгоритма нечеткого логического вывода)

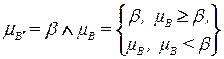, (2.17)

соответствующей множеству .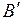

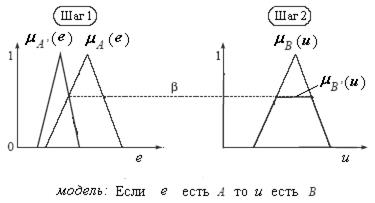
Рис. 2.7,а

Операция (2.12) называется активизацией правила. Весь алгоритм максиминной инференции графически иллюстрируется рис. 2.7,а.

В системах управления 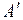представляет собой, как правило, четкое множество, включающее лишь один элемент 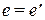(e-четкая (количественная) переменная), и его можно рассматривать как нечеткое множество с ФП

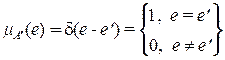, (2.18)

т.е. как синглтон (четкое число). Такой метод определения степени принадлежности называется синглтонной фаззификацией. При этом степень истинности

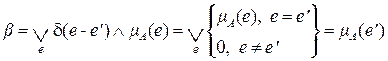, (2.19)

т.е. равна степени принадлежност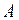и при 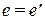, другими словами, степени принадлежности, полученной при фаззификации (см. рисунок ниже).

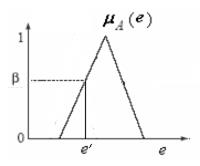
Для случая, когда 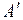есть синглтон с ФП (2.18), то в соответствии с (2.17)

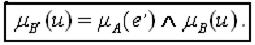(2.20)

В дальнейшем нас будет интересовать в основном только этот случай.

Если нечеткое множество 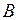− синглтон с ФП

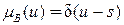, (2.21)

то нечеткое множество 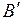будет представлять собой также синглтон с ФП

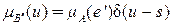. (2.22)