Управление с нечеткой внутренней моделью.

Чтобы преодолеть те проблемы, которые возникают при использовании метода, рассмотренного в предыдущем пункте и связанного с разомкнутой системой, было предложено дополнить структуру с инверсным управлением обратной связью. Это привело к появлению еще одного из возможных путей использования нечетких правил − применению управления с нечеткой внутренней моделью (УВМ). При этом функциональная схема системы управления (рис. 2.4) включает в себя, наряду с объектом управления (ОУ), три элемента: 1) нечеткую модель объекта управления, позволяющую предсказать реакцию ОУ на приложенное к нему управляющее воздействие u(t); 2) нечеткий инверсный контроллер, построенный как обратная нечеткая модель объекта управления; 3) фильтр, расположенный в цепи обратной связи.

Если нечеткая модель точно описывает свойства объекта управления, и отсутствуют (идеальный случай) измеряемое возмущающее воздействие f(t), приведенное к выходу объекта, и не измеряемое возмущающее воздействие f_P(t), сигнал обратной связи 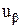(t) равен нулю и система работает как разомкнутая система. В случае, когда модель объекта идеальна, но имеет место измеряемое возмущение, сигнал обратной связи равен 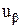(t)= f(t) и не влияет непосредственно на управляющее воздействие, а просто вычитается из задающего воздействия v(t). В результате полностью исключается влияние f(t)

на управляемую

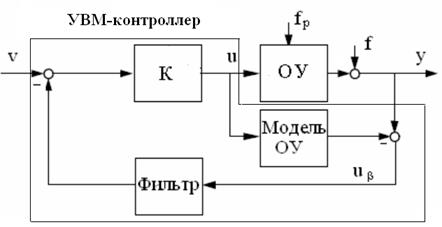
Рис. 2.4

величину y(t). Фильтр вводится в обратную связь с целью повысить робастность системы к неопределенности модели объекта, учитываемой как действие не измеряемого возмущения f_p(t), и к шуму измерения. Если ошибки моделирования большие, то система может стать неустойчивой. При этом за счет фильтра можно избежать неустойчивой работы за счет снижения значений АЧХ разомкнутой системы на высоких частотах.

Однако если ОУ проявляет нелинейные свойства, то нет возможности спроектировать фильтр заранее с учетом ошибок моделирования и возмущающих воздействий. Это обстоятельство представляет собой основную трудность проектирования такой системы.

3 . Управление с моделью предсказания. Кроме управления с внутренней моделью к числу продвинутых принципов управления относят так называемое управление с моделью предсказания (МПУ). Контроллер системы управления с моделью предсказания вычисляет настоящее и будущие значения управляющего воздействия на основе информации о текущем состоянии объекта управления или управляемой величины, чтобы принудить модель (систему) предсказания воспроизводить желаемое задающее воздействие в течение горизонта (интервала) предсказания. Основное достоинство систем МПУ в том, что они объединяют в себе методы оптимального управления, стохастического управления, управления ОУ с запаздыванием (или в общем случае управления нелинейными и многомерными ОУ). Управление, основанное на стратегии предсказания, также демонстрирует высокую робастность по отношению к несоответствию модели и к немоделируемой динамике. Такое управление в каждый момент дискретизации оптимизирует закон управления в отличие от других известных в настоящее время принципов управления. Таким образом, обеспечивая полезный инструмент для управления линейными и нелинейными системами.

Управление МПУ не какая-то специфическая стратегия (закон) управления, а стратегия, соответствующая широкому спектру методов управления, инспирированных некоторыми общими ключевыми принципами.

Каждый контроллер цифровой системы МПУ включает в себя четыре блока (рис.2.4,а).

1. Модель предсказания (прогноза), вытекающую из модели ОУ и позволяющую вычислить будущие значения управляемой величины 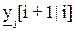={y[i+1|i], y[i+2|i],…, y[i+j|i]} на конечном горизонте [i,i+j]. Например, для линейного объекта управления, описываемого четкой моделью

,

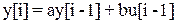модель предсказания имеет вид

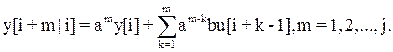
Символ |i говорит о том, что для получения прогнозируемых значений используется текущее (настоящее) значение управляемой величины y[i].

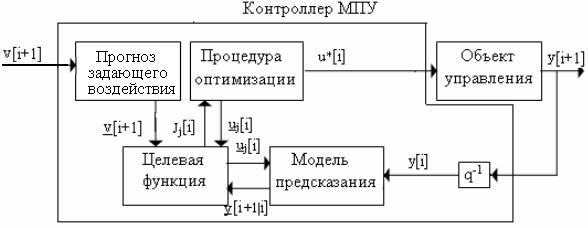
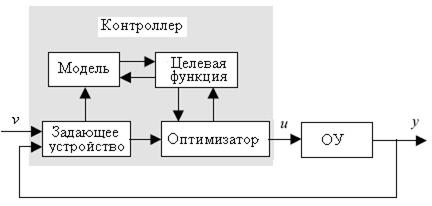
Рис. 2.4,б

Любая модель (типа вход-выход или в переменных состояния), которая описывает динамику ОУ, может быть использована, но в рассматриваемом случае имеется в виду нечеткая (лингвистическая) модель ОУ. Модели возмущающих воздействий и шума измерения (не показаны на схеме) являются частью модели ОУ и служат для предсказания поведения возмущений, влияющих на работу ОУ, а также для повышения робастности системы.

2. Желаемое задающее воздействие как вектор 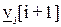, который описывает, каким должен быть выход объекта управления (управляемая величина) в пределах горизонта управления, т.е. в моменты i+1, i+2,…,i+j.

3. Целевая функция (функция стоимости) 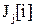, которая выражает требуемые показатели качества работы системы, такие как максимальное абсолютное значение управляющего воздействия 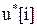, перерегулирование, время переходного процесса и т.д. Другими словами, она определяет свойства замкнутой системы и стратегию управления контроллера. Как правило, целевая функция имеет следующий вид

.

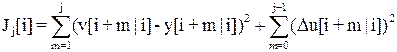4. Процедура оптимизации использует выходную величину модели предсказания 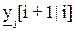для определения управляющего воздействия как вектора 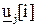в пределах горизонта предсказания, точнее управляющей последовательности 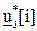={ 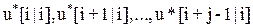} или как вектора разностей управляющей последовательности 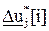={ 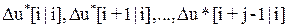}, путем минимизации целевой функции. Цель заключается в том, чтобы минимизировать разность между желаемым задающим воздействием 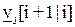и предсказанным значением управляемой величины 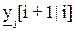в пределах горизонта управления. Выбор этой процедуры зависит от модели предсказания, целевой функции и ограничений, наложенных на величину управляющего воздействия и переменные состояния системы. Обычно ограничения выглядят так:

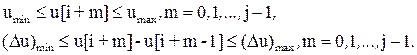
Оператор q^-1 смещает входную последовательность на один период дискретизации в сторону запаздывания.

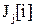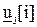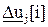В течение периода дискретизации [(i-1)T, iT] процедура оптимизации производит различные вычисления целевой функции для различных векторов будущего управляющего воздействия или . Модель предсказания использует эти будущие воздействия управляющего воздействия, чтобы вычислить будущие значения своего выходного сигнала 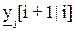. В каждый момент дискретизации модель предсказания инициализируется за счет измерения прошлого значения выхода объекта управления y[i] и будущих значений управляющего воздействия. Когда найден оптимальный вектор управляющего воздействия, его первый элемент 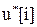или 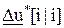поступает на вход ОУ, так что закон управления

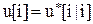или ,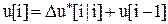

и контроллер ожидает следующего момента дискретизации, i+1, после которого вся вышеописанная процедура повторяется для смещенного на один период дискретизации горизонта предсказания [i+1, i+j+1] и измеренного выхода ОУ y[i+1]. С каждым новым периодом дискретизации горизонт предсказания все дальше удаляется от момента i. Поэтому управление УМП характеризуют как принцип удаляющегося горизонта. Основная идея управления УМП иллюстрирована с помощью рис. 2.4,б.

Лекция 9

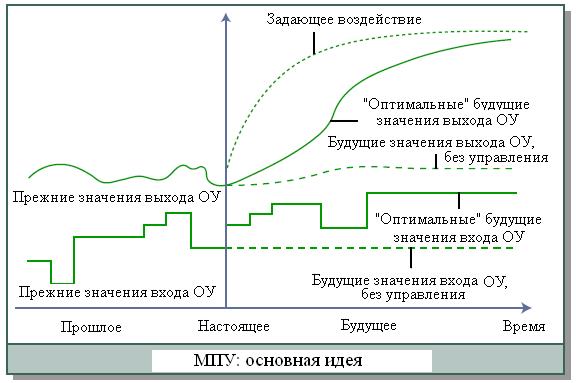
Рис. 2.4,б

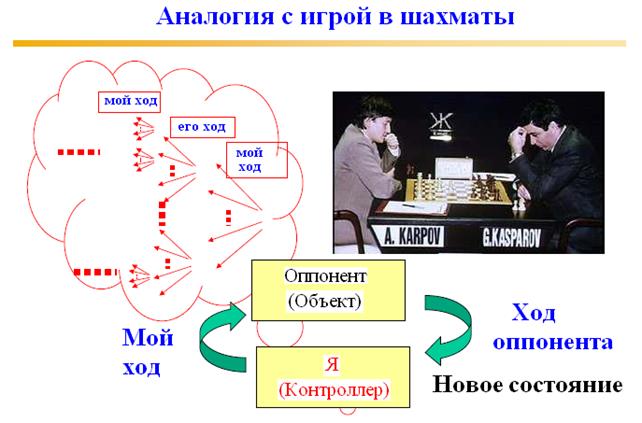
Заметим, что МПУ-управление можно рассматривать как обобщение системы управления УВМ. На рис. ниже МПУ контроллер встраивается в структуру системы управления УВМ с тем, чтобы скомпенсировать возмущения и ошибки моделирования. Очевидно, что нечеткая модель объекта может быть включена в эту схему с одной стороны для предсказания управляемой величины в УВМ системе (модель ОУ), а с другой стороны

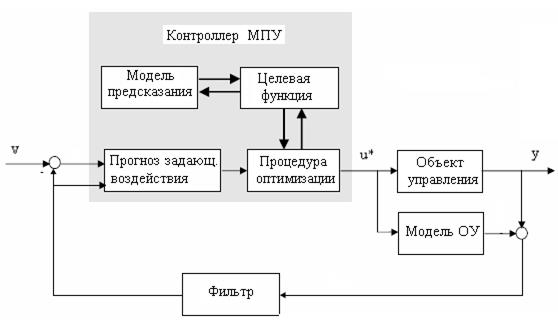
для прогноза будущих значений (модель предсказания), используемых в процедуре оптимизации (стратегия МПУ).

Мы должны иметь в виду, что использование нечетких моделей для предсказания выходов нелинейных объектов означает, что требуется решение задачи невыпуклой оптимизации. Эта время затратная процедура, которая требует значительной мощности компьютера, и большинство методов, связанных с ее решением, не гарантируют получение глобального минимума. В общем случае это обстоятельство затрудняет применение МПУ управления для нелинейных объектов. Однако это общая проблема, характерная для нелинейных систем, не обязательно связанная с нечетким подходом.

Опустить