Основы нечеткой логики

Логика, основанная на двух значениях истинности «Истина» и «Ложь», в ряде случаев оказывается неадекватной, когда идет речь об описании высказываний (утверждений) людей. С целью оценить численно степень истинности высказываний (утверждений) человека нечеткая логика применяет весь диапазон значений истинности от 0 (Ложь) до 1 (Истина). В результате нечеткая логика используется для построения законов управления, реализуемых с помощью нечетких регуляторов в системах автоматики. Отсюда основы нечеткой логики должны знать специалисты в области автоматического управления.

Нечеткий регулятор, применяемый на цементном заводе посредством нечеткой логики, например, стремится подражать (копировать) действиям оператора, обусловленным логикой рассуждений. В качестве иллюстрации рассмотрим расходный бак (резервуар питающей воды), который служит для

питания водой фрезера для разбуривания цементных пробок. При этом должен быть обеспечен постоянный расход жидкости. Упрощенная схема, отображающая процесс, подлежащий управлению (рис. 1.1), включает сам расходный бак, два датчика уровня и электромагнитный вентиль.

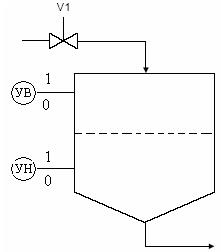
Рис. 1.1

Цель управления вентилем заключается в том, чтобы наполнять бак водой, когда ее уровень ниже, чем УН, и прекращать поступление воды в бак, если ее уровень больше, чем УВ. Выходной сигнал датчика нижнего уровня УН равен 1, когда уровень выше установленного значения УН, и равен 0, когда уровень ниже установленного значения УН. Аналогично можно приписать числовые значения выходному сигналу датчика верхнего уровня УВ. Вентиль открывается, когда входной сигнал V1 принимает значение 1, и закрывается, когда входной сигнал V1 становится равным нулю. В двухзначной (булевой) логике поведение регулятора можно описать следующим законом управления:

V1= 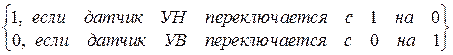. (1.1)

Стратегию оператора, которому поручено управлять положением вентиля, в данном случае можно описать следующим образом:

Если уровень низкий, то открываю вентиль V1, (1.2)

Если уровень высокий, то закрываю вентиль V1.

Стратегия (1.1) пригодна для построения программируемых логических контроллеров (ПЛК) с помощью булевой алгебры, а правила (1.2) применимы для построения нечетких регуляторов, использующих нечеткую логику. Здесь наша цель состоит не в том, чтобы дать детальное описание применения последней (т.е. нечеткой логике), а объяснить на примере, на каком основании строится нечеткая логика.

Лофти Заде, «отец нечеткой логики», утверждал, что большое число (масса) множеств в окружающем нас мире могут быть определены в рамках нечетко заданных (размытых) границ. Действительно, множество высоких гор или множество измерений уровня жидкости, меньших нижнего уровня (рис. 1.1), являются примерами таких множеств. Заде предложил расширить двухзначную логику, определяемую бинарной парой {0, 1}, на весь непрерывный интервал [0, 1] и с этой целью ввел постепенный переход ото лжи к истине.

Оригинальные и пионерские статьи по нечетким множествам, опубликованные им в 1965, 1973, 1975 гг., трактуют теорию нечетких множеств как результат расширения классической теории четких множеств.

Здесь мы сфокусируем свое внимание на теории нечетких множеств и рассмотрим основные определения и операции. Пожалуйста, примите во внимание, что интерпретация нечетких множеств, которая будет представлена вам, является лишь одной из возможных. Заде и другие авторы используют альтернативные определения. В дальнейшем жирными строчными буквами будем обозначать матрицы, например A; жирными прописными буквами - векторы, например x; курсивом – скаляры, например n; жирными прописными буквами – операции, например min.

Нечеткие множества

Нечеткие множества представляют собой развитие математического понятия множества. Впервые множества начал исследовать немецкий математик Георг Кантор (1845-1918). Созданная им теория множеств встречала возражения в течение всей его жизни. Однако в настоящее время большинство математиков поверило в возможность представления многих, если не всех разделов математики на языке теории множеств. Многие ученые обратили внимание на важность «фаззификации» (нечеткости) в теории множеств и большое количество литературы, посвященное этой проблематике, является доказательством такого внимания.

Для специалистов в области управления нечеткая логика и нечеткие отношения являются самыми важными понятиями для того, чтобы разобраться в механизме действия нечетких правил.

Традиционные (общепринятые, четкие) множества.Множество есть любая совокупность элементов (предметов) произвольной природы, которые можно трактовать как единое целое. Кантор описывал множество посредством его членов так, что отдельные предметы из данного универсума (окружающего мира) являются его (множества) членами или нет. Понятия множества, совокупности, класса, так же как понятия предмет, элемент, член являются синонимами. Вообще любое нечто, названное в обыденном разговоре множеством является множеством и в математическом смысле (сравните следующие примеры).

Пример 1.1 (множества).Следующие списки или совокупности предметов хорошо определены, что дает право назвать их множествами:

а) множество неотрицательных чисел меньших чем 4. Это конечное множество с четырьмя элементами 0, 1, 2 и 3;

б) множество живых динозавров в подвалах Палеонтологического музея в г. Москве. Это множество не содержит ни одного элемента и поэтому называется пустым множеством;

в) множество числовых результатов измерения напряжения, превышающих 10 вольт. Хотя это множество является бесконечным множеством, однако нетрудно ответить на вопрос является ли результат данного измерения напряжения его элементом или нет.

Множество можно определить, перечисляя его элементы. Эти элементы полностью характеризуют множество. Список элементов A={0,1,2,3} полностью определяет конечное множество (конечное число элементов). Нельзя перечислить все элементы бесконечного множества. Поэтому мы должны вместо списка указать некоторое свойство, присущее всем элементам множества, например, используя предикат (утверждение) x>10. Такое множество определяется элементами из окружающего мира (универсума), для которых утверждение является истинным. Таким образом, имеются два пути описания множества: явно с помощью списка либо неявно с помощью предиката.

Классическое (четкое) множество имеет четкие границы. Так классическое множество A, фигурирующее в примере в) может быть выражено как

,

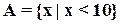что ясно, недвусмысленно говорит о граничном значении, равном 10. При этом , если x меньше, чем это число, то x принадлежит множеству A, в противном случае x не принадлежит этому множеству.

Нечеткие множества.Следуя идеям Заде, заметим, что многие множества для определения своих элементов требуют другие критерии (границы), чем один критерий вида или-или (например, напряжение или меньше или больше 10 вольт). Рассмотрим множество молодые люди. Годовалый ребенок, очевидно, является элементом этого множества, а столетняя персона наверняка не принадлежит к этому множеству. Но что можно сказать о 20-, 30-, 40-летних людях? Еще один пример связан с сообщениями о погоде, касающимися высокой температуры, сильного ветра или благоприятных дней. В других случаях критерий выглядит вроде бы как четкий, но воспринимается как нечеткий: предельная скорость автомобиля 60 километров в час, освободить номер в гостинице в 12 часов дня, 50-летний мужчина. Заде предложил использовать понятие степень принадлежности, чтобы переход от «принадлежности элемента к множеству» к «непринадлежности элемента множеству» был нерезким, а постепенным, плавным, т.е. границы нечеткого множества, что следует из его названия являются нечеткими, размытыми. При этом степень принадлежности, заданная для всех его элементов, называется функцией принадлежности и описывает полностью нечеткое множество. Степень принадлежности конкретного элемента множества представляет собой обычно положительное вещественное число, расположенное в диапазоне от 0 до 1 и часто обозначаемое греческой буквой 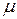. Чем больше такое число, тем больше степень принадлежности. На рис. 1.2 показано в качестве иллюстрации возможное определение нечеткого множества высокий уровень воды в баке с помощью функции принадлежности.

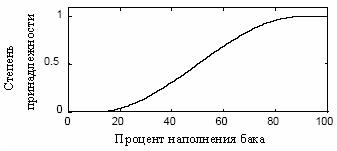
Рис. 1.2

Лекция 2

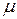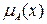Заде рассматривал множество Кантора как особый случай, при котором все элементы x множества A имеют полную степень принадлежности =1, а те, которые не принадлежат множеству, имеют степень принадлежности, равную нулю, т.е. . При этом функция принадлежности такого множества A определяется как (рис. 1.2,а)

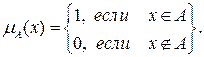
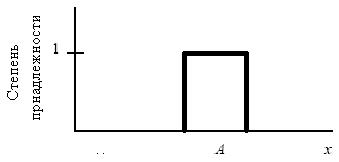
Рис. 1.2,а

Он назвал, между прочим, множество Кантора ненечетким; в настоящее время для такого названия используется термин четкое множество, что позволяет избежать некоторых дилемм (затруднительных положений).

Заметим, что Заде не дал формальной основы для определения степени принадлежности. Степень принадлежности 50- летнего человека к множеству молодой человек зависит от собственной точки зрения. Степень принадлежности является определенным числом, однако, субъективной мерой, зависящей от ситуации (окружающей обстановки) и обстоятельств.

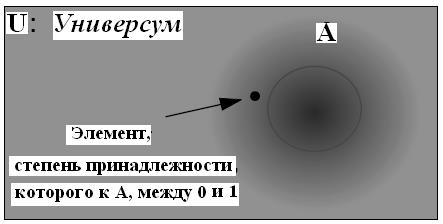
Функция принадлежности отличается от функции распределения вероятностей в связи с тем, что лингвистическая (словесная) неопределенность имеет другую природу по сравнению со статистической неопределенностью. Проиллюстрируем это положение с помощью примера с множеством съедаемых яиц.

Пример 1.2 (Вероятность относительно возможности). Рассмотрим утверждение «Борис съедает за завтраком x яиц», где

.

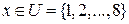Мы можем найти плотность вероятности распределенияp такого события, фиксируя число съеденных Борисом яиц в течение 100 дней:

U = [ 1 2 3 4 5 6 7 8 ]

p = [ 0,1 0,8 0,1 0 0 0 0 0 ].

Нечеткое множество, выражающее степень легкости, с которой Борис съедает за завтраком x яиц, может быть представлено следующей так называемой возможностью распределения ,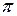

U = [ 1 2 3 4 5 6 7 8 ]

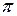= [ 1 1 1 1 0,8 0,6 0,4 0,2 ].

Как видим, для x =3 (съесть 3 яйца) возможность равна 1, а вероятность лишь 0,1.

Пример показывает, что возможность события не является тем же, что его вероятность. Однако, если событие возможно, оно должно быть и вероятным. Вы можете рассматривать функцию принадлежности как ваше субъективное распределение вероятности в противоположность статистическому распределению, построенному на основе экспериментов. Заметим, что нечеткость вызвана не случайностью элементов, входящих во множество, а неопределенностью и неточностью самой природы абстрактных мыслей и понятий.

Универсум

Элементы нечеткого множества выбираются (черпаются) из универсального множества или короче универсума. Универсум включает в себя все элементы, которые можно использовать при рассмотрении множества. В частности в выше рассмотренном примере универсумом является множество

U = [ 1 2 3 4 5 6 7 8 ].

Можно сказать, что универсум является областью определения множества, следовательно, и его функции принадлежности. Тем не менее, универсум зависит от контекста, как показывает следующий пример.

Пример 1.3 (универсум). а) множество «молодые люди» может иметь в качестве универсума всех людей, проживающих на земле. Как альтернативу универсумом можно считать людей, возраст которых лежит между 0 и 100 годами; эти люди будут представлять переменную возраст (рис. 1.3).

Множества «более или менее молодой», «очень молодой» и «не очень молодой» получены из множеств «молодой» и «старый»;

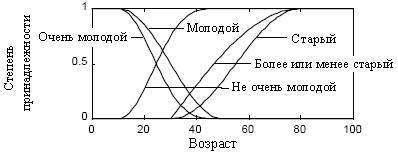
Рис. 1.3

б) множество x >>10 (x много больше 10 вольт) может иметь как универсум все положительные результаты измерений напряжения.

Применение универсума позволяет исключить из рассмотрения ошибочные результаты измерений, например отрицательные значения для уровня воды в баке.

В том случае, когда мы имеем дело с нечисловыми переменными, например, с переменной вкус пищи, которые не могут быть измерены в отношении численного масштаба, мы не можем использовать в качестве универсума множество чисел. При этом элементы универсума должны быть взяты, как говорят, из психологического континуума(сплошной среды); для данного примера таким универсумом может быть {горький, соленый, кислый, сладкий,…}.

Определение (нечеткое множество). Если U есть набор элементов (другими словами, универсум), обозначаемых традиционно x, то нечеткое множество A в U определяется как упорядоченное множество пар:

,

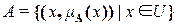где 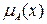называется функцией принадлежности (ФП) x к A.