Лінеаризована модель СД

Лінеарізованну модель СД отримаємо на підставі відомого рівняння кутової характеристики трифазного явнополюсного двигуна:

; ;

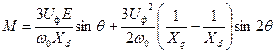Це рівняння свідчить про те, що момент СД складається з двох складових:

- синхронний

- реактивний (асинхронний).

Аналізуючи рівняння, видно, що:

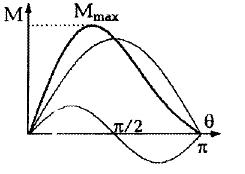
1. реактивний момент збільшує крутизну робочої ділянки кутової характеристики і трохи підвищує перевантажувальну здатність двигуна;

2. реактивний момент залежить від квадрата напруги;

3. синхронний момент лінійно залежить від напруги.

Це означає, що робочу ділянку кутової характеристики можна замінити лінійною залежністю, що проходить через точку номінального режиму:

,

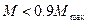
Диференціюючи отримаємо наближене рівняння динамічної механічної характеристики

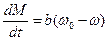
На підставі властивостей СД можна скласти механічну модель, що відображає особливості двигуна

.

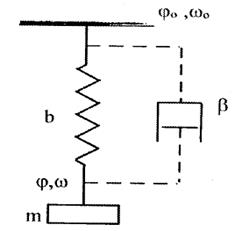
Тут електромагнітний зв'язок замінений механічною пружиною з жорсткістю b, приведенийний момент інерції масою m. Наявність демпферної обмотки і створюваний нею асинхронний момент при гойданнях (малих коливаннях швидкості ); 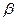- динамічна жорсткість.

З урахуванням останнього рівняння для кутової механічної характеристики можна записати:

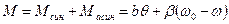
де

;

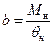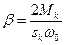
Структурна схема моделі:

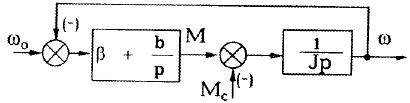
Ця схема отримана у відповідності з наступними викладеннями:

Так як ,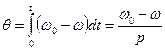

То ,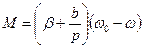

Розглянемо докладніше роботу СД в режимі малих відхилень швидкості. Це може мати місце при входженні в синхронізм, ударному додатку навантаження і .т.п.

У сталому режимі всі моменти, що розвиваються, повинні врівноважувати момент опору.

Рівняння руху ротора

Синхронний момент, спрощено

Перепишемо для режиму малих відхилень 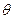від середнього сталого значення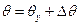

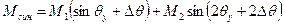
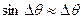При малих має місце і .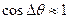

Тоді отримаємо

Асинхронний момент, представлений лінійною залежністю

З урахуванням

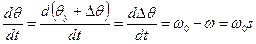
То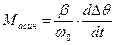

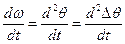
З урахуванням всіх виразів отримаємо

Цим рівнянням описується рух ротора СД в режимі мяскраво-червоних коливань. Рішення рівняння навколо крапки статичної рівноваги з втягуванням

в синхронізм

де 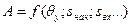, 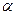- коефіцієнт загасання (речовинний корінь характеристичного рівняння) ;

- частота коливань

- частота свободных колебаний; 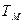- електромеханічна постійна часу.