Уравнение Шрёдингера
Поскольку, по идее Де-Бройля, движение микрочастицы связано с некоторым волновым процессом, Шрёдингер сопоставил ее движению комплексную функцию координат и времени, которую он назвал волновой функцией и обозначил 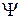 . Часто это функцию так и называют – «пси-функция». В 1926 году Шрёдингер сформулировал уравнение, которому должна удовлетворять
. Часто это функцию так и называют – «пси-функция». В 1926 году Шрёдингер сформулировал уравнение, которому должна удовлетворять 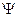 :
:
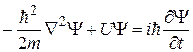 . (33.13)
. (33.13)
В этом уравнении:
m – масса частицы;
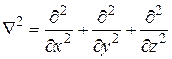 ;
;
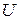 – функция координат и времени, градиент, который с обратным знаком определяет силу, действующую на частицу.
– функция координат и времени, градиент, который с обратным знаком определяет силу, действующую на частицу.
Уравнение (33.13) называется уравнением Шрёдингера. Отметим, что уравнение Шрёдингера не выводится из каких-либо дополнительных соображений. Фактически оно является постулатом квантовой механики, сформулированным на основе аналогии уравнений оптики и аналитической механики. Фактическим обоснованием уравнения (33.13) Является соответствие результатов, полученных на его основе экспериментальным фактам.
Решая (33.13), получают вид волновой функции, описывающей рассматриваемую физическую систему, например, состояния электронов в атомах. Конкретный вид 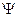 - функции определяется характером силового поля, в котором находится частица, т.е. функцией
- функции определяется характером силового поля, в котором находится частица, т.е. функцией 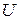 .
.
Если силовое поле стационарно, то 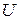 не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шрёдингера распадается на два множителя, один из которых зависит только от координат, другой – только от времени:
не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шрёдингера распадается на два множителя, один из которых зависит только от координат, другой – только от времени:
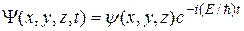 . (33.14)
. (33.14)
где 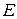 – полная энергия системы, которая в случае стационарного поля остаётся постоянной.
– полная энергия системы, которая в случае стационарного поля остаётся постоянной.
Подставив (33.14) в (33.13), получим:
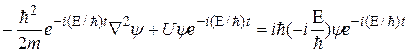
После сокращения на ненулевой множитель 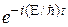 получаем уравнение Шредингера, справедливое в указанных ограничениях:
получаем уравнение Шредингера, справедливое в указанных ограничениях:
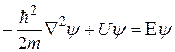 . (33.15)
. (33.15)
Уравнение (33.15) называется уравнением Шрёдингера для стационарных состояний, которое обычно записывают в виде:
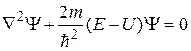 . (33.16)
. (33.16)
В квантовой механике широко используется понятие оператора. Под оператором подразумевают символ, указывающий правило, посредством которого одной функции, 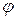 , сопоставляется другая – f:
, сопоставляется другая – f:
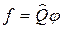 . (33.17)
. (33.17)
(Оператором можно считать набор символов, например, sin(), который подразумевает действия, которые необходимо совершить, чтобы рассчитать синус выражения в скобках. Так оператор 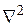 означает, что необходимо найти сумму вторых частных производных по координатам.)
означает, что необходимо найти сумму вторых частных производных по координатам.)
Обозначим
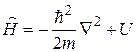 . (33.18)
. (33.18)
Оператор 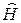 называется оператором Гамильтона (гамильтонианом)
называется оператором Гамильтона (гамильтонианом)
Воспользовавшись этим обозначением, уравнению (33.15) можно придать вид:
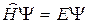 . (33.19)
. (33.19)
Решение уравнения (33.18) позволяет найти возможные значения параметра 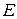 и вид волновых функций, соответствующих им. Параметр
и вид волновых функций, соответствующих им. Параметр 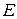 в (33.18) имеет смысл энергии рассматриваемой системы. Допустимые значения параметра соответствуют возможным значениям энергии системы (собственным значениям). Поэтому говорят, что оператор Гамильтона является оператором энергии. А уравнения Шрёдингера вида (33.18) называют уравнениями Шредингера для собственных значений.
в (33.18) имеет смысл энергии рассматриваемой системы. Допустимые значения параметра соответствуют возможным значениям энергии системы (собственным значениям). Поэтому говорят, что оператор Гамильтона является оператором энергии. А уравнения Шрёдингера вида (33.18) называют уравнениями Шредингера для собственных значений.
В квантовой механике каждой физической величине (динамической переменной) 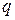 сопоставляется оператор, который обычно обозначают соответствующей прописной буквой
сопоставляется оператор, который обычно обозначают соответствующей прописной буквой 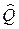 . Например, операторы координат, импульса, момента импульса и т. д. С использованием каждого оператора можно записать уравнение, аналогичное по виду (33.18). Решая такие уравнения (т.е. уравнения типа (33.18)
. Например, операторы координат, импульса, момента импульса и т. д. С использованием каждого оператора можно записать уравнение, аналогичное по виду (33.18). Решая такие уравнения (т.е. уравнения типа (33.18) 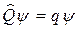 ), находят собственные значения
), находят собственные значения 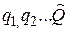 .
.
Дата добавления: 2021-01-11; просмотров: 533;











