ДЕКОМПОЗИЦИЯ АСИНХРОННЫХ КОНЕЧНЫХ АВТОМАТОВ

Структуру асинхронного конечного автомата можно представить в виде последовательного соединения двух блоков (рис. 1).

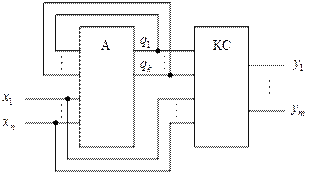
Рис. 1

Блок А представляет собой конечный автомат, который формирует функцию переходов в соответствии с заданной таблицей переходов, а блок КС представляет собой комбинационную логическую схему, которая формирует выходные сигналы (функцию выхода). Методы синтеза комбинационных схем, в том числе и декомпозиционные, достаточно хорошо известны и не рассматриваются в настоящей работе.

Декомпозиция АП – это операция, связанная с разделением синтезируемого устройства на составные части. Составные части также являются конечными автоматами, причём каждая из составляющих будет проще, чем исходная структура. В дальнейшем это позволит упростить процедуру структурного синтеза АП.

Для оценки сложности схемы можно использовать величину

,

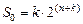где 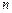– количество входов, а 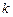– количество выходов внутренних переменных. Указанная величина отражает количество бит информации, необходимое для полного описания таблицы переходов синтезируемого АП. Сложностью устройства, состоящего из нескольких блоков будем считать суммарную сложность всех входящих в него блоков.

Можно выделить два основных вида декомпозиции АП (по способу соединения разделённых блоков) – параллельную (рис. 2) и последовательную (рис. 3).

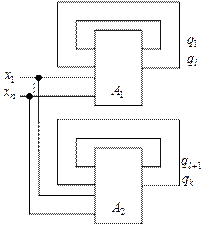
Рис. 2

В случае параллельной декомпозиции сложность схемы после разделения оценивается следующей величиной:

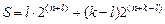
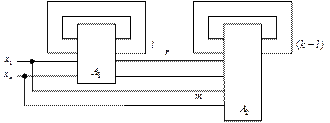
Рис. 3

В случае последовательной декомпозиции сложность схемы после разделения оценивается следующей величиной ( 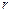– число связей между автоматами):

;

;

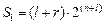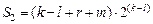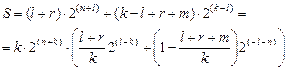
ПАРАЛЛЕЛЬНАЯ ДЕКОМПОЗИЦИЯ

Наиболее простой является параллельная декомпозиция, поскольку АП разделяется на две взаимно независимые структуры: внутренние переменные автомата 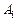не зависят от внутренних переменных автомата 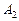и наоборот. Таким образом, для проведения параллельной декомпозиции необходимо проверить наличие фиктивной зависимости внутренних переменных от соответствующих входных аргументов и исключить таковые из логических последовательностей, описывающих автоматы 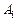и .

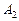Рассмотрим проведение указанной операции на примере. Структурная схема КА задана в виде рис. 4, а его описание – таблицей переходов в виде табл. 1.

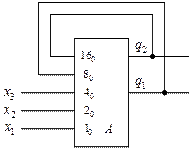
Рис. 4

Таблица 1

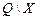
	(0)	(0)		(0)		*	*	*
		(1)	(1)	(1)	(1)	(1)	(1)
		(2)		(2)		(2)	(2)	(2)
		(3)	(3)	(3)	(3)	(3)	*	*

В рассматриваемой таблице переходов не указаны состояния выходных сигналов автомата, поскольку предполагается, что они формируются соответствующей комбинационной логической схемой (КЛС) как функции полного состояния КА, и не влияют на процесс декомпозиции.

Разорвём обратные связи и, развернув таблицу переходов по строкам, получим логическую последовательность КЛС, формирующей функцию переходов.

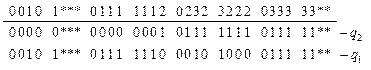
Результаты анализа зависимости выходов от входов приведены в табл. 2.

Таблица 2

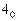
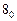
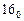
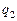
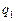
Из табл. 2 видно, что внутренняя переменная 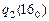фиктивно зависит от входной переменной 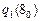и наоборот, следовательно, в данном случае возможна декомпозиция на два независимых автомата 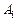и .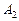

Для нахождения логической последовательности автомата 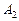, который будет соответствовать внутренней переменной 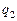, необходимо последовательность 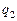разложить в матрицу по переменной 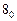. В полученной таким образом матрице будет содержаться две не противоречащие друг другу строки. Логическая последовательность функции переходов автомата 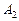представляет собой одну из доопределённых строк матрицы разложения (0000 0001 1111 1111).

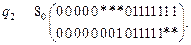
Таблица переходов автомата 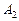может быть получена из указанной логической последовательности путём её разложения в матрицу по старшей входной переменной 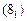, поскольку она соответствует выходу внутренней переменной рассматриваемого автомата (табл. 3).

Таблица 3

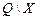
	(0)	(0)	(0)	(0)	(0)	(0)	(0)
		(1)	(1)	(1)	(1)	(1)	(1)	(1)

Аналогично находится и таблица переходов автомата 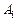(табл. 4), но в данном случае из логической последовательности 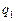исключается фиктивная переменная .

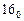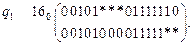
Таблица 4

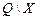
	(0)	(0)		(0)		(0)	(0)	(0)
		(1)	(1)	(1)	(1)	(1)	(1)

Структурная схема синтезированного устройства представлена на рис. 5. В данном случае отпадает необходимость в противогоночном кодировании состояний, поскольку каждый из разделённых автоматов имеет одну внутреннюю переменную, зависящую только от входных сигналов 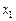, 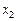и .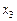

Рис. 5

Для автоматов 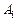и 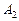возможна минимизация таблиц переходов по столбцам, поскольку они содержат по три различных столбца из восьми. При этом на входе схемы выделяется комбинационный блок 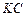, осуществляющий преобразование входных сигналов 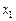, 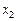и 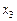в управляющие сигналы минимизированных автоматов 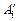и 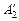(рис. 6).

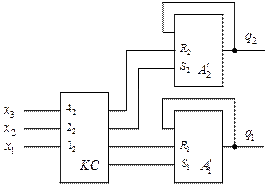
Рис. 6

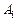Логическая последовательность указанного блока определяется путём кодирования столбцов таблиц переходов автоматов и 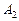, а таблицы переходов автоматов 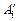и 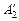образуются путём исключения повторяющихся столбцов соответствующих матриц переходов. Следует заметить, что таблицы переходов автоматов 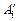и 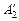получаются одинаковыми, поскольку исходные таблицы 3 и 4 содержат одинаковые столбцы, и совпадают с таблицей переходов 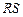-триггера (табл. 5).

Таблица 5

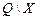
	(0)	(0)		*
		(1)	(1)	*

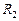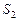Кодирование столбцов табл. 3 позволяет получить последовательность двух старших выходов и блока 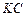(0111 1112), а кодирование столбцов табл. 4 – двух младших выходов 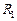и 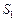(0121 2110). Результирующая логическая последовательность всего блока 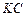получается объединением двух указанных последовательностей с учётом их старшинства (0565 6558).

Гораздо больший практический интерес представляет подход к параллельной декомпозиции АП, связанный с кодированием состояний внутренних переменных. Как уже было сказано выше, при разделении автомата на две части выходы внутренних переменных должны быть взаимно независимыми в том смысле, что при изменении состояния внешних входов изменение состояния выходов внутренних переменных автомата 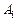не влечёт за собой изменение состояния выходов внутренних переменных автомата 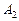(рис. 2). Это может быть достигнуто соответствующим кодированием состояний синтезируемого АП.

ПОКРЫТИЕ АСИНХРОННЫХ КОНЕЧНЫХ АВТОМАТОВ

Структурно асинхронные конечные автоматы могут быть реализованы в двух вариантах [Угрюмов]:

– в виде комбинационной логической схемы (КЛС), охваченной системой обратных связей (с включёнными в цепях обратной связи элементами задержки), вследствие чего в них проявляются свойства запоминания состояний;

– в каноническом представлении в виде соединения двух частей – памяти и комбинационной логической схемы, формирующей функции возбуждения элементов памяти и выходные сигналы.

ПОКРЫТИЕ КОМБИНАЦИОННЫМИ ЛОГИЧЕСКИМИ СХЕМАМИ

Один из вариантов структурной реализации асинхронных конечных автоматов в виде комбинационной логической схемы (КЛС), охваченной системой обратных связей приведён на рис. 12.

Рис. 12

На входы КЛС поступают внешние входные сигналы 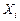и сигналы внутренних переменных 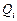, характеризующие состояния АП. На выходе КЛС формируются выходные сигналы 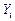и сигналы перевода АП в новое состояние 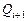. Элементы асинхронного АП переключаются под непосредственным воздействием изменений информационных сигналов 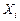, а скорость распространения процесса переключений в цепях асинхронного автомата определяется собственными задержками элементов КЛС. В таком случае идеализированные элементы задержек из цепей обратных связей можно исключить.

Условимся считать входы внутренних переменных 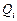более старшими по отношению к внешним входным переменным 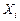, причем самым старшим входом КЛС будет являться самый старший выход внутренних переменных. Если разорвать обратные связи, то получится комбинационная схема с 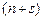входами и 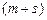выходами. При этом внутренние переменные становятся внешними (рис 2).

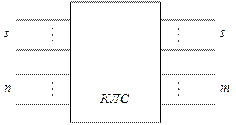
Рис. 13

Выходная логическая последовательность рассматриваемой комбинационной схемы получается развертыванием по строкам совмещенной таблицы переходов синтезируемого автомата, поскольку строкам таблицы соответствуют состояния автомата, а столбцам – комбинации входных сигналов. Полученная таким образом логическая последовательность содержит 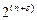элементов, каждый из которых представляет собой 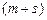-разрядное двоичное число.

Для корректного построения схемы АП необходимо проверить условие возможности замыкания обратных связей. Для этого необходимо разложить логические последовательности каждого из выходов внутренних переменных по соответствующим входным переменным и проверить отсутствие в матрице разложения столбца .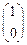

Матрица разложения по входной переменной с весом 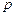строится следующим образом: в первую строку записываются элементы логической последовательности, для которых входная переменная 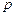равна 0, а во вторую строку – элементы последовательности, для которых входная переменная 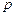равна 1.

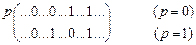
В общем случае в построенной таким образом матрице разложения может присутствовать всего четыре различных столбца.

Столбец 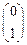соответствует устойчивому состоянию автомата (то есть 0 на входе порождает 0 на выходе, 1 на входе порождает 1 на выходе).

Столбцы 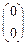и 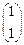соответствуют переходам АП из одного устойчивого состояния в другое (рассматриваемый выход фиктивно зависит от входной переменной с весом ).

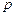В этом случае можно замыкать между собой соответствующие входы и выходы.

При наличии в матрице разложения столбца 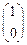схема будет являться генератором (то есть 0 на входе порождает 1 на выходе, а 1 на входе порождает 0 на выходе и т. д.). В таком случае обратную связь замыкать нельзя.

Далее, используя известные методы, необходимо реализовать соответствующую комбинационную схему на требуемых логических элементах и замкнуть разорванные ранее обратные связи. В результате получится схема асинхронного конечного автомата, соответствующего заданной таблице переходов.

В качестве примера рассмотрим реализацию двоичного счетчика-делителя на 2 ( 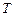-триггера) на мультиплексорах типа 4/1 и на элементах «2И-НЕ».

Временные диаграммы, описывающие поведение синтезируемого автомата и процесс построения свободной от критических состязаний таблицы переходов (этап абстрактного синтеза) рассмотрены выше (рис. 3 и табл. 19).

Из указанной таблицы видно, что функция выхода 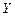не противоречит состоянию младшего разряда внутренней переменной 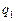. Структурная схема рассматриваемого автомата может быть представлена в виде рис. 4.

Рис. 14

Присвоим входным переменным значения весовых коэффициентов (индекс 0 в обозначении входной переменной свидетельствует о том, что эта переменная является входной для синтезируемой схемы):

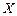– вес 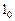(внешняя входная переменная),

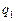– вес 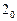(младший разряд внутренней переменной, выходной сигнал),

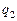– вес 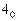(старший разряд внутренней переменной).

Разрываем обратные связи и строим логическую последовательность комбинационной схемы путём развёртывания по строкам таблицы переходов синтезируемого автомата.

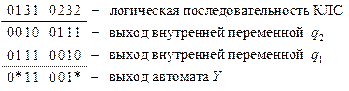
Проверим условие возможности замыкания обратных связей, разложив последовательност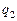и и 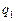по соответствующим входным переменным ( 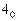и ).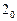

Столбца 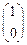в матрицах разложения нет, следовательно, возможно замыкание указанных обратных связей.

РЕАЛИЗАЦИЯ СХЕМЫ СЧЕТЧИКА-ДЕЛИТЕЛЯ НА 2 НА МУЛЬТИПЛЕКСОРАХ ТИПА 4/1

Для реализации синтезируемого устройства на сдвоенном мультиплексоре 4/1 разложим последовательност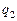и и 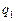по каждой из входных переменных (будем использовать транспонированные матрицы, поскольку их проще построить, и подсчитывать различные столбцы) [5].

Вариант 1.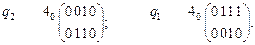

Вариант 2.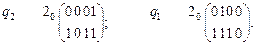

Вариант 3.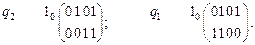

В данном случае наиболее приемлемым для реализации является вариант 2, поскольку в этом варианте отсутствует столбец 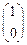, соответствующий инверсии выделенной входной переменной 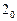, и не требующий включения в схему дополнительного инвертора. Результирующая схема счетчика-делителя на 2 на сдвоенном мультиплексоре 4/1 приведена на рис. 15.

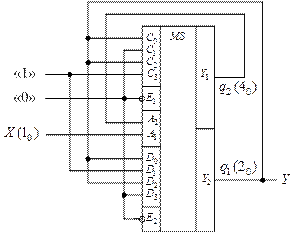
Рис. 15

РЕАЛИЗАЦИЯ СХЕМЫ СЧЕТЧИКА-ДЕЛИТЕЛЯ НА 2 НА ЭЛЕМЕНТАХ «2И-НЕ»

Структурная схема синтезируемого счетчика-делителя может быть представлена в виде параллельного соединения двух трёхвходовых блоков 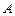и 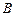, каждый из которых имеет по одному выходу (рис. 16).

Рис. 16

Логические последовательности блоков 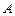и 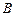, соответствующие внутренним переменным 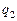и 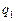были определены выше.

Проведем синтез рассматриваемого устройства методом многоуровневой декомпозиции [5 – 8].

Построим матрицы разложения для блока .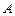

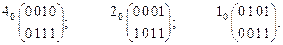
Все три варианта матриц разложения имеют в своем составе по три различных столбца, поэтому выделение двухвходового последовательного блока невозможно. Для проведения начального этапа детализации удобно взять первый или второй варианты, поскольку в них отсутствует столбец 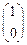. При этом на выходе схемы выделяется трёхвходовый блок, имеющий наиболее простую схемотехническую реализацию (рис. 17).

Рис. 17

На втором этапе детализации разделяем выходной трёхвходовый блок по варианту, имеющему на выходе элемент типа «ИЛИ», поскольку для покрытия используются элементы «2И-НЕ», относящиеся к этому же типу (рис. 18).

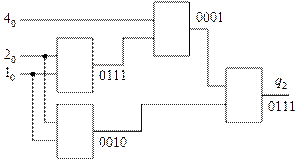
Рис. 18

Построим матрицы разложения для блока .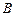

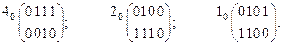
Все три варианта матриц разложения имеют в своем составе по три различных столбца, поэтому выделение двухвходового последовательного блока невозможно. Для реализации удобно использовать первый вариант, поскольку в этом случае схема выхода 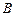будет содержать блоки с последовательностями 0111 и 0010, уже имеющиеся в схеме 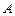(рис. 19).

Рис. 19

На втором этапе детализации разделяем выходной треёвходовый блок по варианту, имеющему на выходе элемент типа «ИЛИ». Схема детализированного блока 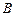представлена на рис. 20.

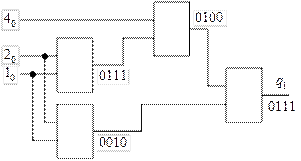
Рис. 20

После объединения схем блоков и получается общая схема проектируемого устройства (рис. 21).

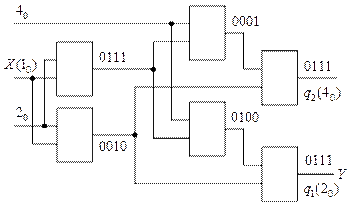
Рис. 21

Далее детализированная схема покрывается заданными логическими элементами «2И-НЕ» (рис 22).

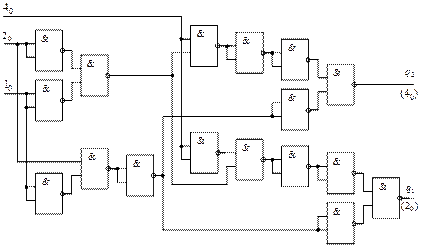
Рис. 22

Поскольку процедура покрытия носит формальный характер, получившаяся схема содержит избыточные элементы. Поэтому после покрытия выполняется оптимизация схемы с целью исключения указанных элементов [5]. На первом этапе удаляются цепочки последовательно соединенных инверторов и элементы с одинаковыми входами (рис 23).

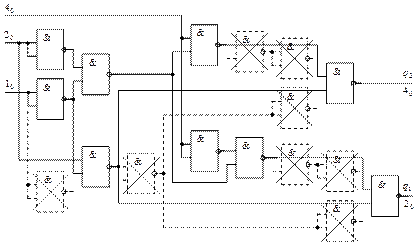
Рис. 23

Присвоим оставшимся после первого этапа оптимизации элементам буквенные обозначения и проведем анализ схемы (рис 24).

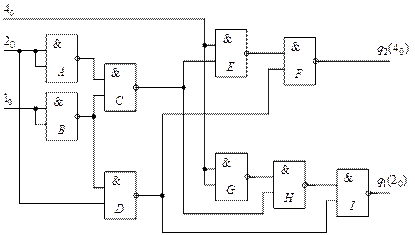
Рис. 24

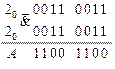
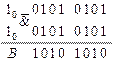
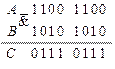
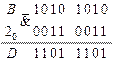
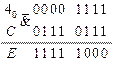
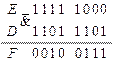
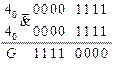
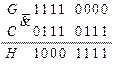
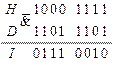
Последовательности, полученные в результате анализа на выходах элементов 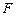и 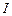полностью совпадают с заданными логическими последовательностями блоков 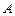и 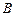, следовательно, схема синтезирована верно.

На втором этапе оптимизации рассмотрим элемент 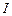(он находится прямо на выходе схемы) с учётом возможной недоопределенности его входных логических последовательностей. Для этого зафиксируем последовательность на одном из его входов (например, поступающую с выхода элемента 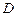) и попробуем подобрать такую последовательность 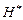, поступающую на другой вход, чтобы выходная последовательность элемента 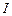не изменилась.

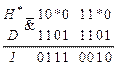
Для формирования последовательности 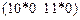, которую можно подать на вход элемента вместо последовательности 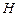, фиксируем последовательность 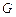и подбираем последовательность .

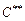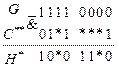
Найденная таким образом последовательность 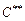не противоречит логической последовательности входной переменной 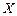, имеющей весовой коэффициент .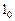

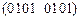Аналогично для элемента 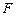– фиксируем выходную последовательность элемента 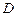и подбираем последовательность .

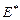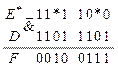
Для формирования последовательности 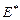фиксируем на входе элемента 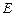последовательность 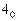и подбираем последовательность .

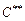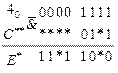
Найденная таким образом последовательность 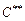также не противоречит логической последовательности входной переменной 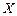, имеющей весовой коэффициент .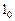

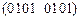Следовательно, на нижние входы элементов 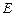и 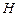можно подать входной сигнал 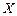. Это позволяет исключить из схемы элементы 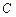и 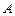(рис. 25).

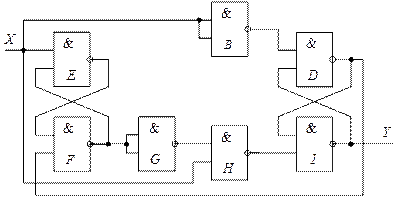
Рис. 25

Построенная описанным выше способом схема, представляющая собой по сути дела 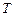-триггер, кардинально отличается от «классических» схем 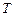-триггеров, приведенных в литературе [1]. Как правило, для построения подобных устройств используется двухступенчатый синхронный 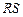-триггер со схемами управления, который можно реализовать на девяти элементах «2И-НЕ». Анализ схемы с использованием временных диаграмм, приведённых на рис. 26, и моделирование в программе ModelSim позволяют сделать вывод о правильности работы синтезированной схемы.

Рис. 26

Проведём повторный анализ схемы с учётом внесённых в схему изменений.

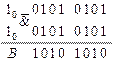
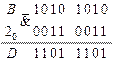
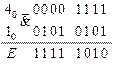
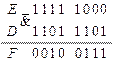
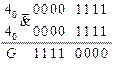
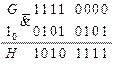
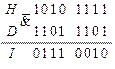
Попытаемся провести второй этап оптимизации для элемента 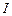ещё раз. Для этого зафиксируем последовательность, поступающую с выхода элемента 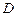и попробуем подобрать новую последовательность 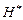, чтобы выходная последовательность элемента 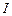не изменилась.

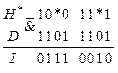
Для формирования последовательности 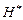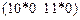, которую можно подать на вход элемента 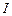вместо последовательности 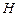, фиксируем последовательность 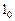и подбираем последовательность .

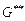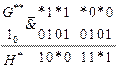
Найденная таким образом последовательность 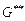не противоречит логической последовательности, формируемой на выходе элемента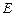 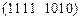. Следовательно, элемент 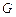из схемы можно исключить, а на верхний вход элемента 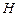подать сигнал с выхода элемента .

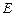После замыкания разорванных ранее обратных связей получаем окончательную схему счетчика-делителя на 2 ( 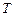-триггера), реализованную на элементах «2И-НЕ» (рис. 27).

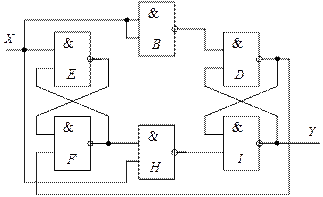
Рис. 27

Анализ схемы с использованием временных диаграмм, приведённых на рис. 28, и моделирование в программе ModelSim (рис. 29) позволяют сделать вывод о работоспособности синтезированной схемы.

Рис. 28

Рис. 29

К недостаткам рассматриваемой схемы можно отнести разные по времени задержки при переключении выходного сигнала из 0 в 1 и из 1 в 0 относительно переднего фронта входного сигнала .

Следует заметить, что при использовании современной схемотехнической базы – программируемых логических интегральных схем (ПЛИС) – зачастую отпадает необходимость в покрытии синтезированных схем, поскольку все известные двухвходовые элементы содержатся в библиотеках САПР и спроектированную схему можно реализовать без покрытия в виде, приведённом на рис. 21.

РЕАЛИЗАЦИЯ ТРИГГЕРНЫХ УСТРОЙСТВ НА ПРОСТЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ

Можно привести формальный способ построения триггерных устройств на примере схемы асинхронного -триггера. В качестве исходного описания функционирования -триггера, как элементарного конечного автомата, используется рассмотренная выше совмещённая таблица переходов и выходов (табл. 8).

Функция выхода не противоречит состоянию памяти (то есть функция выхода совпадает с функцией переходов). Структуру рассматриваемого элементарного автомата можно представить в виде рис. 30.

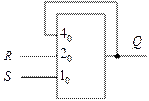
Рис. 30

Если разорвать обратную связь, то получится комбинационная схема с тремя входами и одним выходом. Будем считать, что внутренняя переменная имеет весовой коэффициент 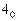, вход 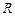– 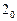, а вход 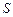– 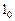(рис. 3). Развернув таблицу переходов по строкам, получаем логическую последовательность комбинационной схемы, реализующей 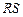-триггер – .

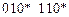Попытаемся провести последовательную декомпозицию, для чего построим матрицы разложения по каждой из входных переменных [3 – 6].

; ; .

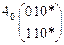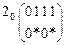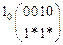В первом варианте матрицы разложения три различных столбца, следовательно, выделение двухвходового последовательного блока невозможно. Во втором и в третьем вариантах в случае соответствующего доопределения звёздочек возможно выделение последовательных блоков.

Рассмотрим вариант 2. Доопределяем звёздочки нулями и для определения последовательности старшего блока производим кодирование столбцов матрицы по элементам первой строки – 0111. Последовательность младшего блока получается развёртыванием по строкам сокращённой матрицы – 0100. В результате получается схема, приведённая на рис. 31.

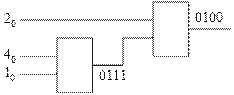
Рис. 31

В третьем варианте можно доопределить звёздочки единицами и произвести кодирование столбцов матрицы по элементам первой строки для определения последовательности старшего блока – 0010. Последовательность младшего блока получается развёртыванием по строкам сокращённой матрицы – 0111. В результате получается схема, приведённая на рис. 32.

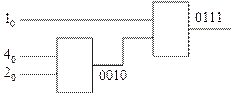
Рис. 32

Производим покрытие детализированной схемы рис. 31 логическими элементами «2И-НЕ» (рис. 33).

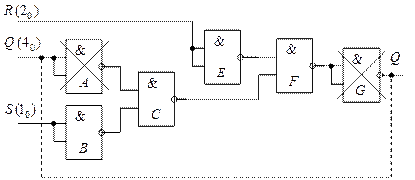
Рис. 33

Восстанавливаем разорванную обратную связь, исключаем цепочки последовательно соединённых инверторов (рис. 33) и перерисовываем схему в привычном виде (рис. 34).

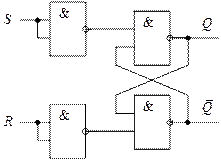
Рис. 34

Полученная таким образом схема асинхронного 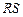-триггера на элементах «2И-НЕ» приводится в любом учебнике по цифровой схемотехнике [1, 2].

Покрытие другого варианта детализации схемы 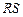-триггера (рис. 32), приведено на рис. 35.

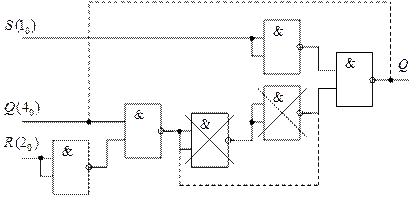
Рис. 35

После исключения цепочки из двух инверторов и восстановления обратной связи, также получается «классическая» схема асинхронного 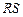-триггера, приведённая на рис. 34.

Аналогично можно построить схему синхронного 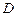-триггера, функционирование которого рассмотрено выше и может быть описано таблицей переходов в виде табл. 9.

Структурная схема 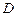-триггера приведена на рис. 36.

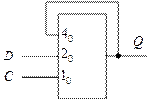
Рис. 36

Логическая последовательность комбинационной схемы, реализующей рассматриваемую функцию, получается путём развёртывания матрицы переходов по строкам – .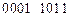

Разорвём обратную связь и попытаемся провести последовательную декомпозицию указанной логической последовательности, для чего построим матрицы разложения по каждой из входных переменных [3 – 6].

; ; .

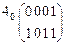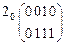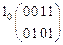В каждой из полученных матриц по три различных столбца, поэтому выделение двухвходового последовательного блока невозможно. Для проведения детализации возьмём первый вариант, поскольку в нём отсутствует столбец 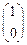. Схема, полученная на первом этапе детализации, приведена на рис. 37.

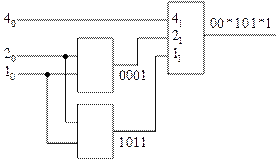
Рис. 37

На втором этапе детализации проводим разделение выходного трёхвходового блока по варианту, имеющему на выходе блок типа «ИЛИ» (для более удобного покрытия элементами «2И-НЕ», рис. 38).

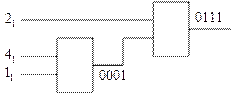
Рис. 38

Окончательная детализированная схема синхронного 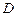-триггера приведена на рис. 39.

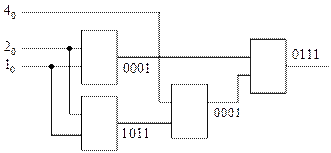
Рис. 39

После покрытия этой схемы логическими элементами «2И-НЕ» получается схема, приведённая на рис. 40.

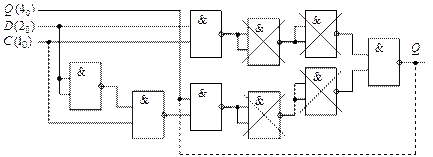
Рис. 40

После исключения цепочек инверторов и восстановления разорванной обратной связи, получается схема синхронного 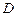-триггера, приведённая на рис. 41.

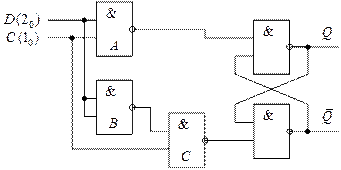
Рис. 41

Попытаемся провести оптимизацию полученной схемы с учётом логической недоопределённости [3]. Рассмотрим элемент 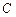, на в<