Квадратичная форма для минимизации
Веса для любого типа кригинга вычисляются минимизацией дисперсии оценивания с соответствующими условиями. Так как дисперсии оценивания являются квадратичными функциями весов, то они называются квадратичными формами. Общий вид минимизируемой дисперсии оценивания для двух проб
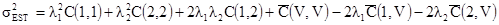 [7.51]
[7.51]
где C(1,1)=C(2,2)=1. Это можно записать, как
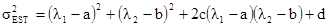 [7.52]
[7.52]
где
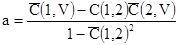 [7.53]
[7.53]
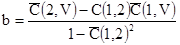 [7.54]
[7.54]
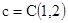 [7.55]
[7.55]
и, где d - подходящее выбранное значение.
На Рис. 7.3 представлено два способа изображения дисперсии оценивания, как функции от весов. Трехмерный график показывает, что это поверхность, имеющая форму раковины. Из уравнения очевидно, что минимум встречается, когда веса принимают значения a и b соответственно, и значение равно d. Читатели могут сами решить SK системы и проверить, что a и b являются весами SK и, что d является дисперсией SK. Изометрические контуры (слева) являются проекцией "раковины".
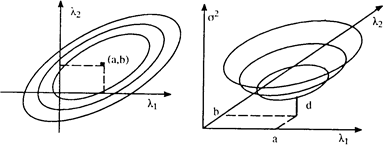
Рис 7.3. Справа трехмерное представление дисперсии оценивания, как функции от весов; слева соответствующие проекции
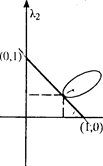
|
Рис 7.4. Линия, представляющая условие OK: 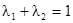 , представлена isovariance контурной линией. Координаты точки, где она касается одного из эллипсов, являются весами OK.
, представлена isovariance контурной линией. Координаты точки, где она касается одного из эллипсов, являются весами OK.
Продемонстрировав минимизацию для простого кригинга, мы теперь обратимся к обычному кригингу. Из-за условий несмещенности сумма весов должна быть равна 1, т.е. 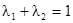 . На Рис 7.4 изображена линия
. На Рис 7.4 изображена линия 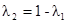 , соединяющая точки (0,1) и (1,0), которая представляет это условие. Минимум встречается в точке, где эта линия касается одного из эллипсов. Соответствующие значения весов – это OK веса, а высота в этой точке – это дисперсия OK. Так как это обычно не является низом раковины, то высота в этой точке больше, чем дно. Другими словами, дисперсия OK больше или равна дисперсии SK. Это также можно увидеть с помощью уравнения. Подстановка
, соединяющая точки (0,1) и (1,0), которая представляет это условие. Минимум встречается в точке, где эта линия касается одного из эллипсов. Соответствующие значения весов – это OK веса, а высота в этой точке – это дисперсия OK. Так как это обычно не является низом раковины, то высота в этой точке больше, чем дно. Другими словами, дисперсия OK больше или равна дисперсии SK. Это также можно увидеть с помощью уравнения. Подстановка 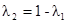 в квадратичную форму дает
в квадратичную форму дает
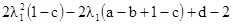 [7.56]
[7.56]
Это можно переписать, как
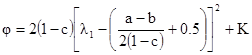 [7.57]
[7.57]
Отсюда становится понятно, что минимум дисперсии оценивания достигается тогда, когда первый вес равен:
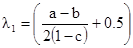 [7.58]
[7.58]
Читатель может проверить, что это просто другая форма записи первого веса OK.
Упражнения
Упр 7.1 Чистый эффект самородка. Пусть мы имеем пробы в двух точках (1,0) и (2,0) и хотим оценить величину пространственной переменной в произвольной точке (x,y). Вариограммой является чистый эффект самородка с порогом 1.0. Вычислите веса обычного кригинга и дисперсию кригинга. Рассчитайте, какие веса будут для N проб.
Все веса будут равны. Поэтому кригинговая оценка будет средне арифметическим значений проб. Кригинг не может дать больше деталей, потому что даже соседние точки некоррелированы. Поэтому данные используются здесь только для оценивания общего среднего пространственной переменной.
Что произойдет в этом случае, если значение среднего известно и используется простой кригинг?
Упр 7.2 Сферическая вариограмма. Как и раньше, у нас две пробы в точках (1,0) и (2,0), и мы хотим оценить значение в произвольной точке (x,y). Но в данном случае вариограмма сферическая с порогом 2.0 и зоной 0.75. Докажите, что веса обычного кригинга определяются следующим образом
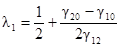 и
и 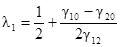 [7.59]
[7.59]
где g20 и g10 обозначают значения вариограммы между одной из точек проб и произвольной точкой, а g12 обозначает значение вариограммы между точками проб.
Нарисуйте круг с радиусом 0.75 (т.е. на величину зоны) вокруг каждой пробы. Снаружи этой зоны нет корреляции между интересующей нас точкой и пробами, и оба веса равны 0.5. Результаты такие же, как и для чистого эффекта самородка. Все, что можно оценить в этом случае, является общим средним.
Упр 7.3 Экспоненциальная вариограмма. Как и раньше у нас две пробы в точках (1,0) и (2,0), и мы хотим оценить величину произвольной точки (x,y). В этот раз вариограмма экспоненциальная с порогом 2.0 и масштабным параметром - 1. Вычислите веса обычного кригинга и дисперсию кригинга. Повторите вычисления для случая, когда порог равен 4, оставляя параметр масштаба таким же. Хотя удвоение порога увеличивает дисперсию кригинга в два раза, веса кригинга остаются такими же.
Упр 7.4 Линейная вариограмма – нехватка памяти Марковина. Как и раньше, есть две пробы в точках (1,0) и (2,0), но вариограмма - линейная с произвольным наклоном. Объектом оценивания является пространственная переменная в точке (x,0), лежащая на оси x. Покажите, что, если целевая точка левее первой точки, (1,0), то ее вес обычного кригинга равен 1.0, а другой - равен нулю, и сделайте то же для точки, лежащей правее второй точки.
Этот пример можно распространить на случай, когда на линии есть несколько проб. Если целевая точка лежит слева от первой точки, то вес первой точки равен 1, а остальных - равен нулю. Аналогично, если целевая точка лежит правее последней точки. Только концевые точки имеют ненулевые веса. Это происходит так, как будто другие пробы были "забыты". Вся доступная информация сосредоточена в концевых пробах. Рассмотрите для себя, что произойдет, если целевая точка лежит между пробами. Обратите внимание: этот эффект происходит только в одномерном пространстве.
Это свойство называется свойством Марковина (Markovian property). Оно хорошо известно в теории временных рядов, особенно в науке о финансах. Например, предполагается, что последняя котировка цены акции отражает всю предыдущую информацию. Такой же эффект используется при выборе цены в модели Блека и Шульза (the Black & Scholes model).
Упр 7.5 Факторизованные вариограммы – перпендикулярный экранирующий эффект. Как и раньше, есть две пробы в точках (1,0) и (2,0). Но в этот раз вариограмма - гауссова с единичным порогом и единичным параметром масштаба. Объектом оценивания является величина пространственной переменной в точке (1,y), лежащей ниже или выше пробы по вертикали. Покажите, что вес простого кригинга второй точки равен нулю. Только точка, находящаяся непосредственно ниже/выше целевой, получает какой-нибудь вес. Этот результат зависит от того факта, что гауссову структуру можно факторизовать по двум компонентам.
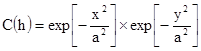 где
где 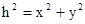 [7.60]
[7.60]
Покажите, что результат также верен для факторизованной экспоненциальной
ковариации:
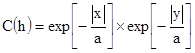 где
где 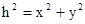 [7.61]
[7.61]
Дата добавления: 2019-05-21; просмотров: 882;











