Кригинг – точный интерполятор

Когда для оценивания значения пространственной переменной в данной точке используются некоторые методы (например, трендовые поверхности), не обязательно, чтобы результат оценивания был точно равен характеристике пробы в этой точке. Методы, которые всегда дают оценку в точке опробования, равную значению пробы, называются точными оценщиками. Следующий пример показывает, что кригинг является точным интерполятором.

Продолжим пример, в котором 5 точек данных использовалось для OK кригинга блока размером 200м на 200м. Теперь мы постараемся оценить содержание в одной из точек опробования (скажем центральной) по всем данным, включая и эту точку. Легко увидеть, что левая часть матрицы точно такая же, как и раньше. Изменился только вектор в правой части. Новая система имеет вид

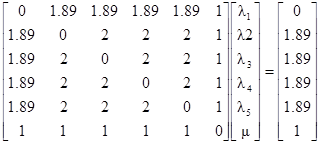[7.49]

Ее можно легко рассчитать, и в результате получаем

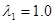
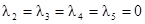[7.50]

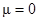
Соответствующая дисперсия кригинга равна нулю. Этот результат не является сюрпризом. Интуитивно понятно, что оценка, которая минимизирует дисперсию оценивания, является действительной величиной пробы. Этот результат определяется тем, что элементы первой колонки и первой строки равны соответствующим элементам вектора правой части.

Если ко всем слагаемым в матрице и в векторе добавить константу (т.е. эффект самородка, представляющий ошибку измерений), то это можно учесть, используя ряд единиц в последнем ряду матрицы.

Иногда люди ошибочно путают это свойство кригинговой оценки с процедурой перекрестной проверки модели вариограммы (variogram crossvalidation procedure). Пожалуйста обратите внимание на то, что в описываемом здесь случае, точка для оценивания включена в начальные данные, тогда как точка данных, используемая для процедуры кроссвалидейшн, исключена из начальных данных в тот период, пока оценивается ее значение. Техника кроссвалидейшн обсуждается в деталях в следующей главе.