Определение вариограммы

В главе 2 вариограмма внутренней, случайной функции определена как:

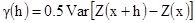[3.1]

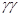
Для стационарных и внутренних переменных среднее Z(x+h)-Z(x) – нуль, и поэтому g(h) -только среднее квадрата разности. Следовательно,

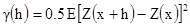[3.2]

Здесь x и x+h относятся к точкам в n-мерном пространства, где n может быть 1, 2 или 3. Например, когда n=2 (т.е. на плоскости), x обозначает точку (x₁, x₂) и h – вектор. Следовательно, вариограмма – это функция от двух компонент h₁ и h₂, или альтернативно, от модуля вектора h и его ориентации. Для зафиксированного направления вариограмма показывает, как изменяются значения исследуемой величины при увеличении расстояния между точками. Когда направление изменяется, с помощью вариограммы можно определить анизотропию массива. На рисунке 3.1. показана типичная вариограмма.

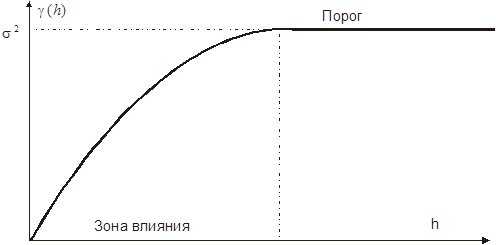
Рис 3.1. Типичная вариограмма, которая достигает предела, называемого порогом (sill), на расстоянии, называемом зоной влияния (range)

Вариограмма имеет следующие особенности:

- Она всегда начинается с нуля (для h=0, Z(x+h)=Z(x)). Она может прерываться только после начала.

- Она обычно возрастает с увеличением h,

- Она возрастает до некоторого уровня, называемого порогом, и затем становится плоской. Иногда она может возрастать и дальше.

Свойства вариограммы сейчас будут рассмотрены в деталях.