Рамка № 2 : Доказательства свойств ковариации.

Первое свойство. Для стационарных переменных среднее m существует. Ковариация равна, по определению:

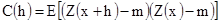[2.10]

Подстановка h=0 дает

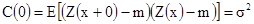[2.11]

Второе свойство. По определению

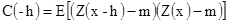[2.12]

Подставляя t=x-h, получаем

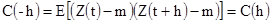[2.13]

Третье свойство. Для доказательства третьего свойства мы должны показать, что

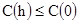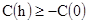и [2.14]

Мы начнем с неравенства

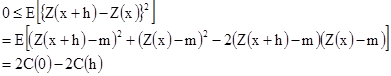[2.15]

Отсюда 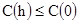[2.16]

Аналогично можно получить другое неравенство, если начать с выражения

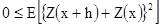
Отсюда 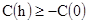[2.17]

В результате мы получили

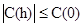[2.18]

Это называется неравенством Шварца (Schwartz’s inequality).

Понятно, что это становится возможным только тогда, когда вариограмма ограничена сверху порогом. Можно математически доказать, что ограниченные сверху вариограммы получаются только для стационарных пространственных переменных. Правильнее будет сказать, что только стационарные пространственные переменные имеют вариограммы с порогом. Следовательно, беспороговые вариограммы получаются из внутренних или нестационарных пространственных переменных.

Наконец можно доказать, что для стационарных и внутренних переменных

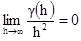[2.19]

Этот результат нелегко доказать. Интересующиеся читатели могут обратиться к Матерону (1972). Уравнение означает, что, если вариограмма возрастает быстрее, чем квадрат h, то переменная нестационарная.

Упражнения

Выражение дисперсий в терминах ковариаций. Одним из ключевых элементов геостатистики является выражение дисперсии линейной комбинации (взвешенного среднего) в понятиях весов и ковариационной функции, и позже - вариограммы. Первое упражнение выводит основную формулу; во втором – она применяется к частному случаю.

Упр 2.1. Пусть Z(x) стационарная случайная функция. Ее пространственная ковариация обозначена C(h). Пусть Z* взвешенное среднее значений в двух точках:

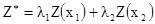[2.20]

где l₁ и l₂ – два весовых коэффициента и x₁ и x₂ – две точки. Какое будет ожидаемое значение Z*? Выразите ее дисперсию в терминах весовых факторов и ее ковариации C(h).

Теперь обобщите это для произвольной комбинации Z**

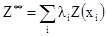[2.21]

Какое ожидаемое значение Z**? Покажите, что ее дисперсия может быть записана другим образом:

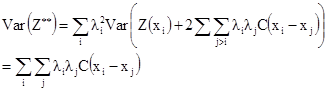[2.22]

Упр 2.2. Пусть Z(x) – стационарная, случайная функция, и пусть Z* взвешенное среднее значений величин в четырех углах квадрата со сторонами 100м на 100м:

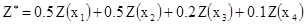[2.23]

Оценить дисперсию Z*, если пространственная ковариация Z(x) экспоненциальная:

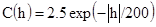[2.24]

(В следующей главе мы увидим, что это приемлемая модель для ковариации).

Вариограмма

Содержание

Эта и следующая глава посвящены вариограмме. В первой главе после определения вариограммы обсуждаются ее теоретические свойства (например, зона влияния, поведение около начала, анизотропия, присутствие тренда и т.д.). Представлены основные модели вариограмм. Чтобы проиллюстрировать разницу между моделями, приведены примеры вариограмм для некоторых видов переменных. Доказывается формула для вычисления дисперсии линейной комбинации пространственных переменных в терминах вариограммы. Подчеркивается причина, почему только положительно определенные функции могут быть использованы в качестве моделей для вариограмм.