Функция пространственной ковариации

До подробного рассмотрения свойств вариограммы, мы представим некоторые основные свойства пространственной ковариации и определим связь между ней и вариограммой для стационарных случайных функций. (Отметьте: не существует ковариации для случайной внутренней функции, которая не стационарна). Три важных свойства ее перечислены ниже. Доказательство приведено в Рамке № 2.

C(0)=s² [2.5]

C(h)=C(-h) [2.6]

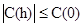[2.7]

Отметьте, что в некоторых выражениях появляются абсолютные значения, потому что ковариация может иметь отрицательные значения. Наше следующее задача - установить связь между вариограммой и соответствующей ковариационной функцией:

g(h)=C(0)-C(h) [2.8]

Доказательство. Доказательство начнем с определения вариограммы:

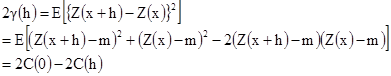[2.9]

Отсюда результат. Он показывает, что соответствующая ковариация получается “перевертыванием вариограммы сверху вниз”. Рисунок 2.2. иллюстрирует эту идею.

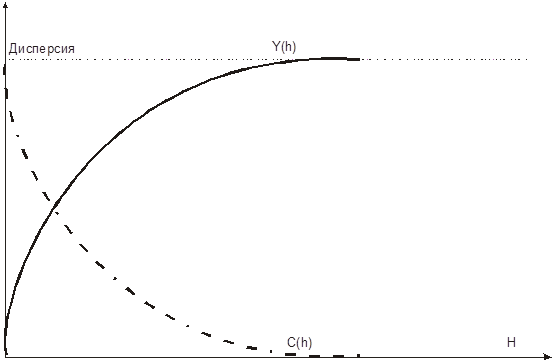
Рис 2.2. Вариограмма начинается с нуля и возрастает до значения порога

(дисперсии), а пространственная ковариационная функция начинается от дисперсии и уменьшается до нуля.