Математический маятник

Математический маятник — это идеализированная система, представляющая собой материальную точку на невесомой и нерастяжимой нити. Хорошим приближением к этой модели является маленький тяжелый шарик на легкой длинной нити (рис.12.6).

Рис. 12.6

Движение такого маятника происходит под действием двух сил: силы тяжести — 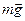и упругой силы натяжения нити — 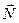. Запишем уравнение второго закона Ньютона в проекции на касательное направление :

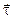–mg Sin j = ma_t. (12.8)

Тангенциальное ускорение a_t связано с угловым ускорением :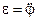

.

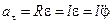Учтя это соотношение, перепишем уравнение движения ещё раз:

,

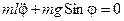или так:

.

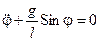При условии «малых колебаний» Sin j » j и уравнение движения приобретает знакомую форму:

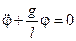. (12.9)

Это дифференциальное уравнение малых колебаний математического маятника. Решение такого уравнения известно — это гармоническая функция:

j = j₀ Cos (wt + a).

Квадрат круговой частоты этих колебаний равен коэффициенту при функции в уравнении (12.9):

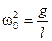, то есть 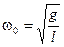. (12.10)

Частота определяется только длиной нити. Период колебаний математического маятника равен:

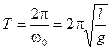. (12.11)