ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ ОБОРОТНОГО МАЯТНИКА
Процессы, обладающие той или иной степенью повторяемости во времени, называются колебаниями. Описывающие их функции времени обладают свойством периодичности. В частности, для механических колебаний таким свойством обладают обобщенные координаты системы, т.е. величины, однозначно определяющие в каждый момент времени положение системы в пространстве, но не обязательно являющиеся декартовыми координатами.
Различают свободные и вынужденные колебания. Свободными называются колебания, которые совершает система, предоставленная самой себе после какого-либо внешнего воздействия. Вынужденными называются колебания, происходящие под действием внешней периодически изменяющейся силы.
Простейшими колебаниями являются гармонические колебания, при которых обобщенные координаты системы изменяются по закону синуса или косинуса. Этот вид колебаний особенно важен, во-первых, потому, что реальные колебания часто имеют характер близкий к гармоническим, а, во-вторых, периодические процессы с другой зависимостью от времени могут быть представлены в виде суперпозиции гармонических колебаний.
Гармонические колебания
В качестве примера рассмотрим движение материальной точки (частицы) массой m под действием упругой силы 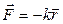 , где
, где 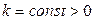 ,
, 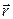 - радиус-вектор частицы относительно положения равновесия.
- радиус-вектор частицы относительно положения равновесия.
Уравнение движения частицы в соответствии со вторым законом Ньютона запишется в виде

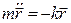 ,
,
или
 . (1)
. (1)
Поскольку момент упругой силы относительно точки 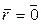
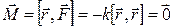 , то момент импульса частицы относительно той же точки
, то момент импульса частицы относительно той же точки 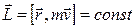 . Поэтому движение будет происходить в фиксированной плоскости, перпендикулярной вектору
. Поэтому движение будет происходить в фиксированной плоскости, перпендикулярной вектору 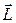 . Введем в этой плоскости систему координат ХОУ с началом в положении равновесия частицы. Тогда, проектируя уравнение (1) на координатные оси, приходим к системе двух независимых дифференциальных уравнений
. Введем в этой плоскости систему координат ХОУ с началом в положении равновесия частицы. Тогда, проектируя уравнение (1) на координатные оси, приходим к системе двух независимых дифференциальных уравнений
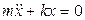 , (2)
, (2)
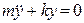 . (3)
. (3)
Будем искать решение уравнения (2) в виде
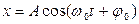 , (4)
, (4)
где  ,
, 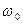 ,
,  - некоторые константы. Дважды дифференцируя функцию (3) по времени, находим
- некоторые константы. Дважды дифференцируя функцию (3) по времени, находим
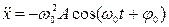 . (5)
. (5)
Подставляя (5) и (4) в (2), получаем
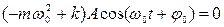 .
.
Поскольку 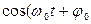 ) не является тождественным нулем, то функция (4) будет решением уравнения (2) при произвольных
) не является тождественным нулем, то функция (4) будет решением уравнения (2) при произвольных  и
и  , но с
, но с
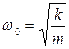 . (6)
. (6)
Движение частицы, описываемое законом (4), называют гармоническими колебаниями.
Постоянную (6), определяющую период функции (4) 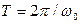 (время одного полного колебания), называют циклической, или круговой частотой колебаний. Интервал времени
(время одного полного колебания), называют циклической, или круговой частотой колебаний. Интервал времени 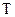 называют периодом колебаний. Функцию
называют периодом колебаний. Функцию 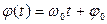 называют фазой колебаний. Константу
называют фазой колебаний. Константу 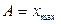 называют амплитудой колебаний. Значения постоянных
называют амплитудой колебаний. Значения постоянных  и
и  определяется из начальных условий
определяется из начальных условий  и
и 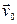 , задающих соответственно начальное положение и начальную скорость частицы.
, задающих соответственно начальное положение и начальную скорость частицы.
Совершенно аналогично решение уравнения (3) запишется в виде
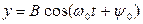 . (7)
. (7)
Функции (4) и (7) определяют кинематический закон движения частицы под действием упругой силы. Вид траектории движения в плоскости ХОУ зависит от начальных условий, а следовательно, от значений констант 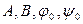 .
.
В частности, если 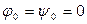 и
и  , то уравнение траектории имеет вид
, то уравнение траектории имеет вид  , и частица совершает гармонические колебания с частотой
, и частица совершает гармонические колебания с частотой 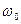 и амплитудой
и амплитудой 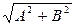 вдоль диагонали прямоугольника со сторонами 2А и 2В (рис.1.6.1). Если же
вдоль диагонали прямоугольника со сторонами 2А и 2В (рис.1.6.1). Если же 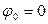 , а
, а 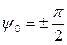 , то уравнение траектории имеет вид
, то уравнение траектории имеет вид
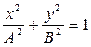 ,
,
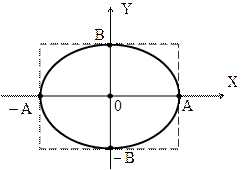
т.е. частица движется по эллипсу с полуосями А и В (рис.1.6.2)
 | |||
 |
Рис.1.6.1 Рис.1.6.2
Таким образом, в данном случае периодическое движение по замкнутой кривой может рассматриваться как суперпозиция двух гармонических взаимно-перпендикулярных колебаний.
Физический маятник
Рассмотрим теорию колебаний физического маятника. Физическим маятником называют твердое тело, совершающее колебания вокруг оси, проходящей через любую его точку, не совпадающую с центром инерции (тяжести) тела. Это механическая система с одной степенью свободы. В

Рис.1.6.3
качестве обобщенной координаты выберем угол отклонения 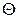 прямой, проходящей через точку подвеса О и центр инерции С (рис.1.6.3), от вертикали (положения равновесия). Будем считать также, что
прямой, проходящей через точку подвеса О и центр инерции С (рис.1.6.3), от вертикали (положения равновесия). Будем считать также, что 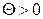 при
при 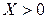 и
и 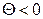 при
при 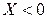 . Допустим, что в рассматриваемый момент времени маятник движется от положения равновесия, т.е.
. Допустим, что в рассматриваемый момент времени маятник движется от положения равновесия, т.е.  , а угловая скорость
, а угловая скорость 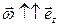 . Момент силы тяжести
. Момент силы тяжести 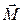 относительно точки О в этом положении противоположен вектору
относительно точки О в этом положении противоположен вектору 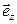 (рис.1.6.3). Поскольку момент силы реакции оси относительно точки 0 равен нулю, то уравнение движения физического маятника запишется в виде
(рис.1.6.3). Поскольку момент силы реакции оси относительно точки 0 равен нулю, то уравнение движения физического маятника запишется в виде
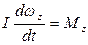 , (8)
, (8)
где I – момент инерции маятника относительно оси Z. Но 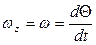 ,
, 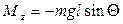 , где
, где  - расстояние от точки подвеса до центра инерции маятника. Следовательно, вместо (8) получаем
- расстояние от точки подвеса до центра инерции маятника. Следовательно, вместо (8) получаем
 ,
,
или 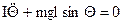 . (9)
. (9)
Если ограничиться случаем малых колебаний т.е. углов отклонения, удовлетворяющих в радианной мере приближенному равенству 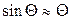 , то уравнение (9) перепишется так:
, то уравнение (9) перепишется так:
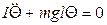 . (10)
. (10)
Сравнивая (10) с (2), заключаем, что общее решение этого уравнения имеет вид
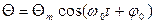 , (11)
, (11)
где 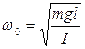 , (12)
, (12)
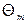 - угол наибольшего отклонения маятника от положения равновесия. Из (12) вытекает, что период малых колебаний физического маятника
- угол наибольшего отклонения маятника от положения равновесия. Из (12) вытекает, что период малых колебаний физического маятника
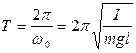 . (13)
. (13)
Таким образом, малые колебания физического маятника являются гармоническими.
Далее замечаем, что отношение 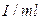 имеет размерность длины:
имеет размерность длины: 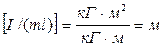 . Учитывая это обстоятельство, введем понятие приведенной длины физического маятника:
. Учитывая это обстоятельство, введем понятие приведенной длины физического маятника:
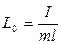 . (14)
. (14)
Тогда формула (13) приобретает особенно простой вид:
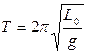 . (15)
. (15)
Приведенная длина физического маятника всегда больше l. Действительно, согласно теореме Штейнера
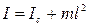 , (16)
, (16)
где 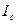 - момент инерции маятника относительно оси, проходящей через центр масс параллельно оси Z (рис.1.6.3).
- момент инерции маятника относительно оси, проходящей через центр масс параллельно оси Z (рис.1.6.3).
Разделив (16) почленно на ml, находим
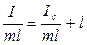 .
.
Но 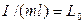 . Поэтому
. Поэтому 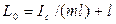 и, следовательно,
и, следовательно, 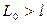 . Точку
. Точку  лежащую на прямой, проходящей через точку подвеса О и центр масс С, на расстоянии приведенной длины от точки О называют центром качания физического маятника. Точка подвеса и центр качания обладают замечательным свойством взаимности: если точку подвеса О и центр качания
лежащую на прямой, проходящей через точку подвеса О и центр масс С, на расстоянии приведенной длины от точки О называют центром качания физического маятника. Точка подвеса и центр качания обладают замечательным свойством взаимности: если точку подвеса О и центр качания  поменять местами, то период малых колебаний физического маятника не изменится. Действительно, новый период колебаний будет равен
поменять местами, то период малых колебаний физического маятника не изменится. Действительно, новый период колебаний будет равен
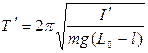 , (17)
, (17)
где 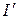 - момент инерции маятника относительно оси, проходящей через точку
- момент инерции маятника относительно оси, проходящей через точку  ,
, 
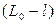 - расстояние от
- расстояние от  до центра масс С. Но согласно теореме Штейнера
до центра масс С. Но согласно теореме Штейнера
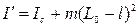 . (18)
. (18)
Вычитая из (18) (16), получаем
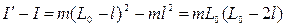 ,
,
откуда с учетом (14)
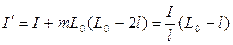 . (19)
. (19)
Подставляя (19) в (17) находим
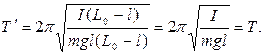
ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
На свойстве взаимности точки подвеса и центра качания основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным называется физический маятник, у которого имеются две параллельные друг другу закрепленные на осевом стержне маятника опорные призмы, за которые он может поочередно подвешиваться (рис.1.6.4).Вдоль того же стержня могут закрепляться и перемещаться тяжелые грузы. Перемещением призм (или грузов) добивают-
 ся того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно приведенной длине
ся того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно приведенной длине 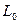 Измерив период колебаний маятника Т и
Измерив период колебаний маятника Т и 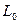 , можно по формуле (15) найти ускорение свободного падения:
, можно по формуле (15) найти ускорение свободного падения:
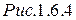
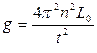 , (20)
, (20)
где t – время n полных колебаний маятника. Таким образом, главная задача прямых измерений, с помощью которых определяется значение ускорения свободного падения, сводится к измерению приведенной длины физического маятника.
Литература
2. Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1987, §§ 49-54,57.
3. Савельев И.В. Курс физики. Т.2. – М.: Наука, 1989. §§ 63-65, 69.
ИЗУЧЕНИЕ ТРЕНИЯ КАЧЕНИЯ С ПОМОЩЬЮ НАКЛОННОГО МАЯТНИКА.
В технике и физике уделяется особое внимание неконсервативным силам, возникающим при качении шара, колеса, цилиндра по плоскости. Эти силы называют силами трения, различают 3 рода сил: ТРЕНИЯ КАЧЕНИЯ, ТРЕНИЯ СКОЛЬЖЕНИЯ и ТРЕНИЯ СЦЕПЛЕНИЯ. В настоящей работе уделяется внимание силам трения качения. Они возникают при движении шаров, цилиндров, колес по поверхности других тел без скольжения, при этом относительная скорость соприкасающихся точек равна 0. Эмпирически Кулон установил, что сила трения качения определяется формулой
 (1)
(1)
где N – сила нормального давления, R – радиус катящегося тела (цилиндр, шар),  - коэффициент трения качения.
- коэффициент трения качения.
Из формулы (1) следует, что коэффициент трения качения – размерная величина в отличие от коэффициента трения скольжения. Этот коэффициент не зависит от скорости качения и радиуса тела, а зависит от материала и состояния поверхности соприкасающихся тел. Так например, при качении дерева по дереву  изменяется в пределах от 0,5 до 0,8 мм; стали по стали от 0,01 до 0,05 мм,
изменяется в пределах от 0,5 до 0,8 мм; стали по стали от 0,01 до 0,05 мм,
Возникновение сил трения качения обусловливается наличием неупругих деформаций, возникающих при движении шаров и цилиндров по поверхности других тел. Чтобы упростить рассуждения предположим, что движение происходит по плоскости и только она деформируется.
 Если цилиндр неподвижен, силы упругости, действующие на каждый малый его элемент со стороны плоскости, будут симметричны относительно вертикальной плоскости ав, проходящей через ось цилиндра (рис.1.7.1). Результирующая сила
Если цилиндр неподвижен, силы упругости, действующие на каждый малый его элемент со стороны плоскости, будут симметричны относительно вертикальной плоскости ав, проходящей через ось цилиндра (рис.1.7.1). Результирующая сила 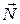 реакции опоры проходит через ось цилиндра и уравновешивает силу тяжести.
реакции опоры проходит через ось цилиндра и уравновешивает силу тяжести.
При качении цилиндра рассмотрим два случая: а) упругой деформации; б) неупругой деформации.
В случае упругой деформации (рис.1.7.2) силы взаимодействия между цилиндром и плоскостью будут совершенно симметричны относительно вертикальной плоскости ав, проходящей через ось цилиндра: каждой силе 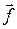 соответствует равная ей сила
соответствует равная ей сила 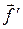 на симметрично расположенном участке площади соприкосновения.
на симметрично расположенном участке площади соприкосновения.
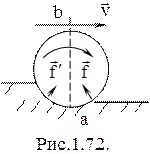 Результирующая всех сил упругой деформации поверхности будет вертикальна и ее момент относительно оси цилиндра также будет равен нулю. Поэтому силы упругих деформаций цилиндра и плоскости при качении не скажутся на скорости качения, и движение будет происходить так, как будто никаких деформаций не было и сил трения качения в этом случае не возникает.
Результирующая всех сил упругой деформации поверхности будет вертикальна и ее момент относительно оси цилиндра также будет равен нулю. Поэтому силы упругих деформаций цилиндра и плоскости при качении не скажутся на скорости качения, и движение будет происходить так, как будто никаких деформаций не было и сил трения качения в этом случае не возникает.
Случай неупругой деформации (что фактически всегда имеет место) дает объяснение возникновения сил трения качения.
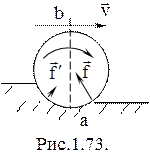 В этом случае силы, действующие на цилиндр со стороны плоскости качения, уже не будут симметричны относительно плоскости ав (рис.1.7.3). Поэтому равнодействующая всех элементарных сил реакции плоскости наклонена к поверхности качения (рис. 1.7.4). Момент этой силы не равен нулю относительно оси цилиндра и противоположен направленно вращения.
В этом случае силы, действующие на цилиндр со стороны плоскости качения, уже не будут симметричны относительно плоскости ав (рис.1.7.3). Поэтому равнодействующая всех элементарных сил реакции плоскости наклонена к поверхности качения (рис. 1.7.4). Момент этой силы не равен нулю относительно оси цилиндра и противоположен направленно вращения.
При этом возникает неравная нулю горизонтальная составляющая, направленная в противоположную сторону движения цилиндра.
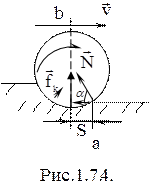 Точка приложения силы
Точка приложения силы 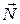 находится впереди плоскости ав (рис.1.7.4), кроме этого линия действия силы
находится впереди плоскости ав (рис.1.7.4), кроме этого линия действия силы 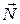 проходит выше центра цилиндра. Горизонтальная составляющая силы представляет силу трения качения:
проходит выше центра цилиндра. Горизонтальная составляющая силы представляет силу трения качения:
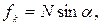 (2)
(2)
вертикальная составляющая - 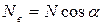 . Расстояние S (см. рис. 1.7.4.) между точкой приложения силы
. Расстояние S (см. рис. 1.7.4.) между точкой приложения силы 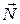 и вертикальной плоскостью мало по сравнению с радиусом цилиндра
и вертикальной плоскостью мало по сравнению с радиусом цилиндра 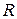 и угол наклона
и угол наклона 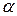 так же мал, следовательно, абсолютная величина
так же мал, следовательно, абсолютная величина  почти равна силе нормального давления цилиндра на плоскость, т.е. весу цилиндра Р. То есть соотношение (2) можно переписать так
почти равна силе нормального давления цилиндра на плоскость, т.е. весу цилиндра Р. То есть соотношение (2) можно переписать так
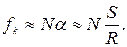 (3)
(3)
Величину S называют “коэффициентом момента силы трения качения”, иногда – плечом трения качения, которое согласно выражению (1) совпадает с коэффициентом трения  .
.
В данной работе коэффициент трения качения определяется методом наклонного маятника по уменьшению со временем амплитуды качений шара на наклонной плоскости.
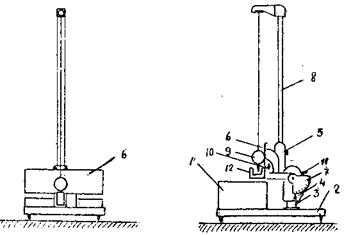
Общий вид наклонного маятника представлен на рис.1.7.5. На основании маятника (2), снабженное четырьмя ножками с регулируемой высотой, установлен миллисекундомер (I). Изменением высоты ножек устанавливают основание (2) в горизонтальной плоскости. В основании закреплена стойка (3), на которой смонтирована червячная передача (4), последняя соединена с кронштейном (5) и воротком (11).
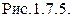 |
Вращая вороток можно менять наклон маятника. Отсчет угла наклона мятника производится по шкале (7), а углов качения маятника – по шкале (6). В кронштейне закреплена стойка (8), на которой подвешивается шар (9) с оськой – держателем. В кронштейне (5) вмонтирован фотоэлектрический датчик (12) и держатель образцов (10). Замена шара производится вывинчиванием оськи - держателя из одного шара и ввинчиванием ее в другой. Управление миллисекундомером производится кнопками "СТОП" и "СБРОС". Качения шара являются затухающими вследствие действия силы трения качения. Закон убывания амплитуды определяется силой, вызывающей затухание. Сила трения качения в широких предела не зависит от скорости, и можно предположить, что амплитуда убывает со временем по арифметической прогрессии. Если пренебречь другими видами диссипативных сил, кроме трения качения, рабочую формулу для определения  можно получить приравняв изменение энергии маятника
можно получить приравняв изменение энергии маятника 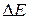 работе А, совершаемой силой трения
работе А, совершаемой силой трения 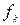 .
.
Пусть Ео и Еn – потенциальные энергии маятника в крайних положениях, отстоящих друг от друга на n полных колебаний, ho и hn высоты центра тяжести шара в соответствующих положениях относительно положения равновесия (рис. 1.7.6). Изменение энергии равно 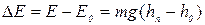 , где
, где 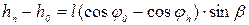 и
и  и
и 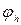 - углы отклонения маятника от положения равновесия в соответствующих положениях,
- углы отклонения маятника от положения равновесия в соответствующих положениях, 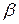 - угол наклона плоскости колебаний. Тогда убыль энергии маятника равна
- угол наклона плоскости колебаний. Тогда убыль энергии маятника равна
 (4)
(4)
Работа, силы трения равна произведению силы трения качения на путь, пройденный телом за n - полных колебаний,
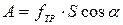 или
или
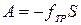 , т.к.
, т.к.
вектор 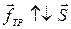 и
и 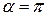 .
.
Пусть S равен
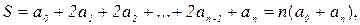 (*)
(*)
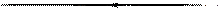 но амплитуда колебаний может быть выражена как длина дуги, опирающаяся на угол
но амплитуда колебаний может быть выражена как длина дуги, опирающаяся на угол 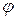 т.е.
т.е. 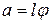 ,
,
тогда 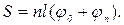 (6)
(6)
(Углы  и
и 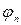 выражаются в радианах).
выражаются в радианах).
С учетом формулы (6) работа силы трения равна
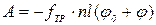 , (7)
, (7)
Подставив в (7) выражение (1) имеем
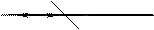
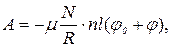
А так как
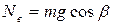
(рис. 1.7.7.), то
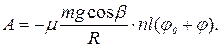
Приравняв изменение энергии маятника 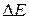 и работу силы трения А получим
и работу силы трения А получим
 .
.
Откуда
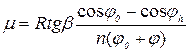 (8)
(8)
Формула (8) является рабочей для расчета коэффициента трения качения
Литература
1. Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1988, §§ 15,19,21,24..
2. Стрелков С.П. Механика. М. Наука, 1965, §§ 38,41,42,75.
Сивухин Д.В. Общий курс физики. – М.: Наука 1974, т.1. §§ 17,24,27.
ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Динамические системы, в которых могут существовать периодические процессы, принято называть колебательными системами. Колебания, происходящие в таких системах, представленных самим себе после некоторого внешнего воздействия, называются свободными. Во всякой реальной колебательной системе имеются силы сопротивления, приводящие к уменьшению ее энергии. Если убыль энергии не компенсируется работой внешних сил, то свободные колебания будут затухать. Колебания, возникающие и происходящие в таких системах под действием периодически изменяющейся внешней силы, получили название вынужденных колебаний.
При рассмотрении внешнего воздействия, возбуждающего колебания в системе, различают силовые и параметрические воздействия. Силовым называют воздействия, при котором остаются неизменными параметры колебательной системы. Напротив, параметрическое воздействие возбуждает колебания в системе при периодическом изменении ее параметров (например, периодическое изменение длины математического маятника). В случае реальных колебательных систем эти воздействия строго разделить нельзя. Поэтому чисто силовые воздействия на колебательную систему имеет место только при определенных условиях, идеализирующих реальную ситуацию.
Рассмотрим незатухающие колебания материальной точки массой m, возбужденные и поддерживаемые периодически изменяющейся силой с малой амплитудой F0 и циклической частотой w
 (1)
(1)
при которой не будет проявляться изменение параметров собственных колебаний материальной точки к и 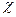 , определяющих соответственно действующие на нее силы упругости и сопротивления
, определяющих соответственно действующие на нее силы упругости и сопротивления
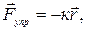 (2)
(2)
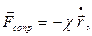 (3)
(3)
где 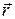 - радиус-вектор частицы относительно положения равновесия,
- радиус-вектор частицы относительно положения равновесия, 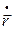 - ее скорость, к и
- ее скорость, к и 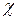 – некоторые положительные константы.
– некоторые положительные константы.
Уравнение движения материальной точки под действием сил (1) – (3) запишется следующим образом
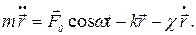 (4)
(4)
Выбирая ось х в направлении вектора 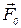 и проектируя уравнение (4) на эту ось, после очевидного преобразования получим
и проектируя уравнение (4) на эту ось, после очевидного преобразования получим
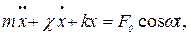 (5)
(5)
или, после почленного деления (5) на m,
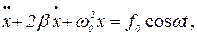 (6)
(6)
где положено  ,
, 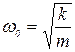 ,
, 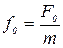 .
.
Параметры 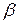 и
и 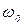 называют соответственно коэффициентом затухания и собственной циклической частотой колебаний (см. лаб. работу №1.6.)
называют соответственно коэффициентом затухания и собственной циклической частотой колебаний (см. лаб. работу №1.6.)
Решением уравнения (6) называют такую функцию 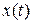 , которая обращает его в тождество, т.е. в равенство, справедливое при любом значении аргумента t из области определения функции
, которая обращает его в тождество, т.е. в равенство, справедливое при любом значении аргумента t из области определения функции 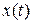 . Будем искать решение уравнения (6) в виде
. Будем искать решение уравнения (6) в виде
 (7)
(7)
где А и 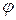 - некоторые константы, выбор значений которых должен обеспечить обращение уравнения (6) в тождество. Для их определения дважды продифференцируем функцию (7) по времени:
- некоторые константы, выбор значений которых должен обеспечить обращение уравнения (6) в тождество. Для их определения дважды продифференцируем функцию (7) по времени:
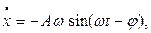 (8)
(8)
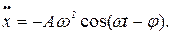 (9)
(9)
Подставляя (7), (8) и (9) в (6), получим
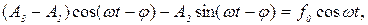 (10)
(10)
где для краткости введены
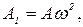
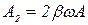 ,
, 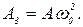 (11)
(11)
Раскрывая далее 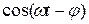 и
и 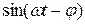 с помощью известных тригонометрических формул, преобразуем (10) к виду
с помощью известных тригонометрических формул, преобразуем (10) к виду

Ясно, что это уравнение будет справедливо при любых значениях аргумента t, если положить
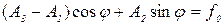 (12)
(12)
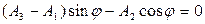 (13)
(13)
Возводя уравнения (12) и (13) в квадрат и складывая их, очевидно получаем
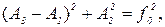
или, с учетом (11)
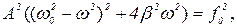
откуда следует, что
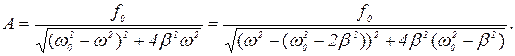 (14)
(14)
Из (14) очевидно вытекает, что если 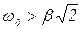 , то
, то
при частоте 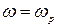 , где
, где
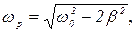 (15)
(15)
амплитуда вынужденных колебаний достигает максимума, определяемого формулой
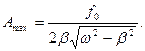 (16)
(16)
Таким образом, зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний становится максимальной. Это явление называется резонансом, а частота (15) и амплитуда (16) – соответственно резонансной частотой и резонансной амплитудой.
Далее из (13) следует, что
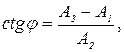
откуда, с учетом (11), получаем
 ,
, 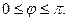 (17)
(17)
Формулы (14) и (17) определяют именно те константы А и 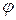 , при которых функция (7) является решением уравнения (6).
, при которых функция (7) является решением уравнения (6).
Следует однако отметить, что общее решение дифференциального уравнения второго порядка должно содержать две произвольные константы, поскольку определение функции по ее второй производной требует двукратного интегрирования. Найденное же нами решение вида (7) с А и 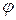 , определяется формулами (14) и (17), такого произвола не содержит. Такое решение дифференциального уравнения называют частным. Частное решение описывает некоторый конкретный процесс из числа всех возможных. Для того чтобы выяснить какой процесс описывается найденным нами решением, необходимо исходить из общего решения уравнения (6). В математике уравнение вида
, определяется формулами (14) и (17), такого произвола не содержит. Такое решение дифференциального уравнения называют частным. Частное решение описывает некоторый конкретный процесс из числа всех возможных. Для того чтобы выяснить какой процесс описывается найденным нами решением, необходимо исходить из общего решения уравнения (6). В математике уравнение вида
 (18)
(18)
где а и b – константы, 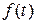 - заданная функция t, называют линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. Если функция
- заданная функция t, называют линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. Если функция 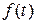 тождественно равна нулю
тождественно равна нулю 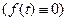 , то уравнение (18) называется однородным. В противном случае – неоднородным. При этом доказывается, что общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и какого – либо частного решения неоднородного.
, то уравнение (18) называется однородным. В противном случае – неоднородным. При этом доказывается, что общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и какого – либо частного решения неоднородного.
В нашем случае однородным уравнением, соответствующим неоднородному уравнению (6), является уравнение вида
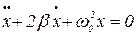 (19)
(19)
Если  , то легко проверить, что его общее решение имеет вид
, то легко проверить, что его общее решение имеет вид
 (20)
(20)
где 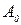 и
и 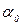 - некоторые произвольные постоянные,
- некоторые произвольные постоянные, 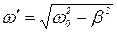 . Поскольку
. Поскольку 
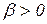 , то функция (20) описывает затухающие колебания с частотой
, то функция (20) описывает затухающие колебания с частотой 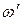 , т.е.
, т.е. 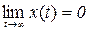 .
.
Таким образом, общее решение уравнения (6) запишется в виде суммы функции (20) и (7), т.е.
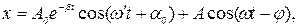 (21)
(21)
где 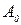 и
и 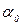 определяются из начальных условий
определяются из начальных условий 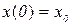 ,
, 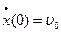 , а
, а 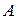 и
и 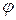 задаются равенствами (14) и (17).
задаются равенствами (14) и (17).
Первое слагаемое в (21) играет заметную роль только в начальной стадии процесса, при так называемом установлении колебаний. С ростом t из-за экспоненциального множителя 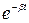 вклад первого слагаемого в сумму все более уменьшается, и по истечении достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (7). Если считать, что
вклад первого слагаемого в сумму все более уменьшается, и по истечении достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (7). Если считать, что 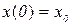 и
и  (т.е. покоящиеся материальная точка начинает колебаться под действием вынуждающей силы), то график функции (21) можно изобразить примерно так
(т.е. покоящиеся материальная точка начинает колебаться под действием вынуждающей силы), то график функции (21) можно изобразить примерно так

Таким образом, найденное нами решение уравнения (6) в виде функции (7) с 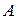 и
и 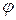 , задаваемыми формулами (14) и (17) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой вынуждающей силы. Для данной колебательной системы (т.е. с заданными
, задаваемыми формулами (14) и (17) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой вынуждающей силы. Для данной колебательной системы (т.е. с заданными 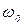 и
и 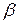 ) их амплитуда зависит от частоты вынуждающей силы
) их амплитуда зависит от частоты вынуждающей силы 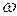 . При этом вынужденные колебания отстают по фазе от частоты вынуждающей силы на величину
. При этом вынужденные колебания отстают по фазе от частоты вынуждающей силы на величину 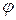 , также зависящую от
, также зависящую от 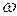 .
.
График функции 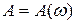 и
и  , задаваемых соответственно формулами (14) и (17), для коэффициентов затухания
, задаваемых соответственно формулами (14) и (17), для коэффициентов затухания  , выглядят примерно так
, выглядят примерно так
 |  |
Совокупность кривых, изображающих зависимость амплитуды и фазы вынужденных колебаний от частоты вынуждающей силы называются соответственно амплитудно–резонансными (рис.1.8.2) и фазово–резонансными (рис. 1.8.3) кривыми.
В основу настоящей работы положена аналогия между вынужденными колебаниями в механической и электрической колебательных системах. В качестве последней используется последовательный RLC–контур, принципиальная схема которого представленна на рис. 1.8.4
Колебательный процесс в контуре возбуждается и поддерживается с помощью генератора звуковой частоты Г, ЭДС которого изменяется с течением времени по гармоническому закону
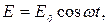 (11)
(11)
где 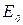 – амплитуда ЭДС,
– амплитуда ЭДС, 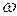 - частота генератора.
- частота генератора.
Дифференциальное уравнение вынужденных колебаний заряда q на обкладках конденсатора С можно, используя закон Ома или правило Кирхгофа, представить в форме, аналогичной уравнению вынужденных колебаний в механической системе :
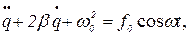 (19)
(19)
где коэффициент затухания
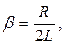 (20)
(20)
сообственная частота
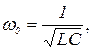 (21)
(21)
а
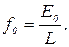 (22)
(22)
Для установившихся колебаний заряда решение уравнения (19) имеет вид
 (23)
(23)
где 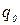 и
и 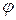 задаются формулами (14) и (17) , в которых
задаются формулами (14) и (17) , в которых 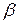 ,
, 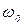 и
и 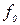 определяются формулами (20) – (22).
определяются формулами (20) – (22).
Разделив формулу (23) почленно на емкость конденсатора С найдем напряженние  на его обкладках, которое подается на вертикальные отклоняющие пластины кинескопа осциллографа О (рис.1.8.5)
на его обкладках, которое подается на вертикальные отклоняющие пластины кинескопа осциллографа О (рис.1.8.5)

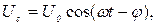 (24)
(24)
где 
На горизонтальные отклоняющие пластины подается напряжение с генератора Г.
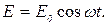 (25)
(25)
При сложении взаимноперпендикулярныых колебаний (24) и (25) на экране осциллографа появляется эллипс, уравнение которого (см. лаб. работу №1.6.) запишится так
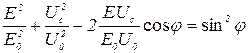 . (27)
. (27)

Ориентация осей эллипса в координатной сетке экрана осциллографа зависит от разности фаз складываемых колебаний 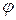 , зависящей в соответствии с (17) от частоты вынужденных колебаний (рис. 1.8.6). Это обстоятельство позволяет построить фазово–резонансные кривые (1.8.3). Действительно, для момента времени, когда
, зависящей в соответствии с (17) от частоты вынужденных колебаний (рис. 1.8.6). Это обстоятельство позволяет построить фазово–резонансные кривые (1.8.3). Действительно, для момента времени, когда 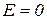 , из (27) вытекает, что
, из (27) вытекает, что
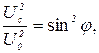 (28)
(28)
где 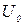 - амплитуда напряжения на конденсаторе,
- амплитуда напряжения на конденсаторе,  - напряжение на конденсаторе, когда выходное напряжение звукового генератора Г равно нулю. Принимая теперь во внимание, что
- напряжение на конденсаторе, когда выходное напряжение звукового генератора Г равно нулю. Принимая теперь во внимание, что
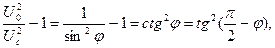
получим удобную формулу для расчета фазового сдвига 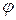 при каждой установленной частоте генератора
при каждой установленной частоте генератора 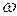 :
:
 (29)
(29)
где знак “+” берется при расположении точек эллипса в A и B квадрантах, и
“-” – при их расположении во II и IV квадрантах (рис.1.8.6).
Значения напряжений 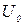 и
и  снимаются с экрана осциллографа как показано на рис.1.8.6.
снимаются с экрана осциллографа как показано на рис.1.8.6.
Литература
1. Савельев И.В. Курс общей физики - М. Наука, 1988. т.1. - §§ 60 – 61.
Дата добавления: 2022-02-05; просмотров: 568;











