Энергия гармонического осциллятора

Собственные незатухающие колебания возникают в системе при выполнении двух условий: во-первых, при смещении из положения равновесия должна возникать возвращающая сила, пропорциональная смещению (упругая или квазиупругая), и, во-вторых, в системе должны отсутствовать диссипативные силы.

Запустить колебание можно по-разному, но в любом случае эта операция означает сообщение системе некоторого запаса энергии. Далее в процессе колебания эта энергия будет переходить из потенциальной в кинетическую и обратно, но сумма этих энергий в любой момент времени должна быть неизменно равной начальной механической энергии.

Обратимся к конкретному осциллятору — пружинному маятнику (рис. 13.1).

Рис. 13.1

Колебание груза массой m происходит по гармоническому закону:

x = a Cos (wt + a). (13.1)

Скорость груза меняется по закону синуса:

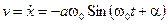. (13.2)

Вычислим механическую энергию маятника в произвольный момент времени t:

E_мех = Е_к + U.

Здесь: 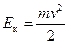— кинетическая энергия груза,

U = 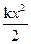— потенциальная энергия деформированной пружины.

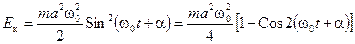(13.3)

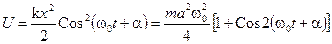(13.4)

В последнем выражении мы учли, что 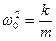, то есть .

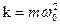Кинетическая и потенциальная энергии осциллятора меняются с частотой, вдвое превышающей частоту колебаний маятника — w₀ (рис. 13.2). И та и другая составляющие механической энергии осциллируют во времени. А их сумма?

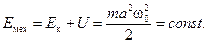(!). (13.5)

Их сумма остается неизменной в любой момент времени. Этот результат можно было бы предсказать a priori: ведь в процессе собственных незатухающих колебаний выполняется закон сохранения механической энергии.

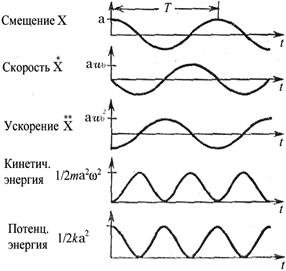
Рис. 13.2

Легко видеть, что уравнение (13.5) выражает механическую энергию системы через максимальную кинетическую, когда потенциальная энергия равна нулю. В этот момент груз проходит с максимальной скоростью положение равновесия.

Но эту же механическую энергию можно связать и с максимальной потенциальной энергией — в точке амплитудного отклонения маятника, где v = 0 и Е_к = 0.

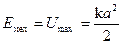. (13.6)

Здесь k = 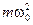, поэтому

.

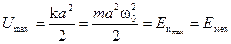Максимальная потенциальная энергия (U_max) незатухающего осциллятора равна его максимальной кинетической энергии 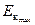и обе они равны полной механической энергии (Е_мех) системы, которая в процессе колебаний остается неизменной.