ЗООТЕХНИЧЕСКИЙ ЭКСПЕРИМЕНТ И МАТЕМАТИЧЕСКИЙ МЕТОД
Умение правильно провести и интерпретировать научный эксперимент совершенно необходимо как ученому, так и работающему в производственных условиях специалисту.
Руководитель производства для проверки новых рекомендуемых приемов, решения различных технологических проблем в животноводстве неизбежно должен осуществлять постановку более или менее обширных опытов. Для научного работника знание методологии научных исследований является основной характеристикой его квалификации.
Процесс научного познания проходит ряд последовательных этапов.
На начальном этапе в результате наблюдений человек накапливает факты относительно того или иного явления в животноводстве, позволяющие формулировать вопросы, представляющие интерес и требующие своего разрешения. Затем следует этап научного поиска путем изучения специальной, в значительной части периодической литературы по интересующему вопросу. Глубокое исследование новейшей литературы позволяет определить состояние вопроса в науке к настоящему времени, степень его изученности. Такое литературное исследование дает возможность получить ответ на ряд вопросов, возникших в процессе наблюдений. Но значительная часть вопросов может остаться невыясненной, что явится основой для постановки задач, подлежащих разрешению в специальном эксперименте.
Эксперимент разрешает глубоко проникнуть в процессы жизнедеятельности животного в условиях всесторонних влияний на него факторов внешней среды, познать его генетические особенности, реакцию на внешние факторы обменных процессов организма. В эксперименте объект исследования ставится в особые, в определенной степени искусственные условия, когда основные факторы внешней среды контролируются, учитываются и точно измеряются. При этом животный объект изучается при воздействии одновременно различных средовых факторов, разной последовательности их влияния, а также во всевозможных сочетаниях. При необходимости эксперимент позволяет повторить исследования при воздействии на животное тех же средовых факторов, а также совместно с другими факторами в тех или иных сочетаниях.
Эксперимент предполагает детально разработанную методику и технику исследования, оснащение его необходимым оборудованием: лабораторными приборами, компьютерами и др.
Целенаправленность исследования, специальные условия для находящихся под опытом животных, направленные варьирования факторов внешней среды, дозированное изменение силы воздействия этих факторов, возможность повторяемости исследований - все это вместе взятое делает эксперимент мощным приемом познания биологической сущности объективных явлений.
Зоотехнический эксперимент имеет особый характер, поскольку в нем биологические факторы сочетаются с факторами технологическими и экономическими.
Основные положения, выводы и закономерности, полученные в эксперименте на ограниченном поголовье животных, требуют крупномасштабного подтверждения в хозяйственных условиях. С этой целью проводится производственная проверка или хозяйственный опыт на большом поголовье животных, в котором имеется возможность выявить технологические и экономические параметры проблемы и рекомендовать их для широкого использования в сельскохозяйственном производстве.
Современная методика опытного дела неразрывно связана с применением методов математической статистики. Какого бы вопроса ни касался эксперимент, его постановка должна обеспечить максимально объективную и статистически достоверную оценку его результатов. В этом отношении весьма показательно положение, что наука только тогда достигает совершенства, когда для ее развития необходима математика. Использование математики придает биологу такие возможности и такой образ мышления, какими он ранее не обладал.
Приложение методов математической статистики к изучению биологических объектов составляет особую науку - биометрию (от греч. "биос" - жизнь и "метрон" - мера). Этот термин введен в 1899 г. английским ученым Гальтоном, впервые использовавшим математический анализ при изучении явлений изменчивости и наследственности. В применении к биологическим, а также и зоотехническим исследованиям математика позволяет решить следующие вопросы:
1. Какова должна быть численность группы животных, отбираемых в эксперимент? Как спланировать эксперимент, определить наиболее приемлемый в конкретном случае метод построения опыта?
2. Как большой объем экспериментальных данных выразить краткими показателями, характеризующими всю подопытную группу животных? Это позволяет получить цифровые данные в четкой и сжатой форме в 2-3 строчках вместо громоздких столбиков таблиц.
3. Как на основе измерений ограниченной группы объектов получить представление о всей совокупности с достаточной точностью и определить эту точность?
4. Как определить взаимосвязи или коррелятивные зависимости между отдельными признаками или явлениями?
5. Как определить влияние отдельных факторов на организм животного или те или иные его признаки, рассчитать возможное взаимодействие при влиянии нескольких факторов на эти признаки?
Объектом исследований в биометрии является не индивидуум, а группа особей. Как статистическая наука биометрия, таким образом, представляет собой область математики, изучающей свойства больших совокупностей, содержащих в себе различные предметы, явления, свойства, признаки и опирается на теорию вероятностей.
Цель настоящего пособия состоит, главным образом, в том, чтобы помочь молодому исследователю овладеть основными статистическими методами. На базе этих знаний исследователь должен уметь правильно спланировать эксперимент еще до его начала, выбрав наиболее подходящую схему опытов и, определив необходимое число объектов для исследования, осуществить математический анализ результатов эксперимента и сделать обоснованные выводы.
Овладение этим математическим аппаратом является, с нашей точки зрения, наиболее сложным и важным элементом в работе молодого экспериментатора. Специалисты зооинженерного образования, как правило, не имеют глубокой математической подготовки, и методы математической статистики им необходимы всего лишь как инструмент для решения конкретных зоотехнических задач. В этой связи основные статистические решения представлены в пособии в форме алгоритмов, которые исследователь должен правильно применять в соответствующих условиях. Алгоритм - это представленная в определенной схеме последовательность действий для нахождения математического решения. Понятие "алгоритм" принято в честь выдающегося узбекского математика Мухамеда бен Муса Хорезми (по арабски аль-Хорезми), жившего в IX в.
Вежливая форма аль-Хорезми в процессе ее применения математиками преобразовалась в термин "алгоритм".
Наряду с широким применением ЭВМ высоких разрешающих возможностей специалист должен понимать сущность расчетов тех или иных математических параметров при условии, что он практически освоит технику этих исчислений. В этой связи в первой части пособия методы расчетов излагаются с ориентацией на "ручные" исчисления и с использованием микрокалькуляторов. Это позволяет хорошо понять существо процесса нахождения тех или иных математических величин, чтобы впоследствии творчески их применять. Вместе с тем, на лабораторных занятиях студенты осваивают практику работы на компьютерах с использованием статистических программ, что описано во второй части пособия.
В пособии для обозначения основных статистических показателей применяется следующая символика:
| xi, mi | - даты, варианты |
| f | - частоты классов |
| a | - условные отклонения |
| A | - условная средняя |
| W | - середина классов |
| к | - классовый промежуток |
| n | - объем выборки, число дат в группе |
| N | - объем генеральной совокупности |
| n | - (ни) число степеней свободы |
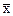 , М , М
| - средняя арифметическая выборочная |
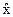
| - средняя генеральная |
| D, d | - знаки разности |
| S, s | - среднее квадратическое отклонение (сигма) |
| S | - (сигма заглавная) - знак суммы |
| V, Сv | - коэффициент вариабельности (%) |
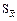 , m , m
| - ошибка репрезентативности средней арифметической |
| t | - показатель (критерий) достоверности суждения, число стандартных отклонений |
| P | - обозначение уровня вероятности |
| S2 | - средний квадрат, девиата, варианса |
| Cx | - дисперсия факториальная |
| Cy | - дисперсия общая |
| Cz | - дисперсия случайная |
| r | - коэффициент корреляции |
| h2 | - (ита квадрат) - степень влияния изучаемых факторов |
| F | - критерий Фишера |
| h | - корреляционное отношение |
| R | - коэффициент прямолинейной регрессии |
РАСПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ПРИЗНАКА. ВАРИАЦИОННЫЙ РЯД И ВАРИАЦИОННАЯ КРИВАЯ
Множество отдельных сходных в основных чертах, но в то же время отличающихся один от другого объектов составляет так называемую совокупность. Совокупностями являются партия цыплят, выведенных в инкубатории в одно время, стадо коров одного хозяйства, поголовье овец одной отары. В совокупность входят отдельные составляющие ее члены или объекты. Число составляющих совокупность объектов называют объемом совокупности, обозначаемым латинской буквой "n". У различных членов совокупности каждый изучаемый признак принимает разные значения, то есть в пределах совокупности варьирует. У отдельных коров одного стада удой за лактацию неодинаков, живая масса поросят одного опороса колеблется и т. д. Значение (меру) признака того или иного члена совокупности называют датой, или вариантой, и обозначают буквой "xi" где буква "i" свидетельствует, что это может быть любая, взятая из совокупности варианта.
В совокупности различные значения признака встречаются неодинаковое число раз: одни чаще, другие реже. Расположение количества объектов соответственно значению признака по мере его порядкового изменения называется распределением признака. Распределение особей по величине признака чаще всего изображается вариационным рядом или вариационной кривой.
Пример. Группа из 100 кур-несушек при индивидуальном учете яйценоскости показала следующую продуктивность за месяц:
| по 15 яиц снесли 4 курицы | |
| -"- 16 | -"- 19 |
| -"- 17 | -"- 34 |
| -"- 18 | -"- 28 |
| -"- 19 | -"- 11 |
| -"- 20 | -"- 4 |
Этот двойной ряд чисел и есть вариационный ряд, состоящий из обозначений классов и соответствующих частот. Вариационный ряд обычно изображается следующим образом (табл.1):
| Таблица 1 | |
| W | f |
В примере приведены целые прерывные вариации, выраженные целым числом, такой ряд называется дискретным. Ряд может быть непрерывным, когда вариации выражаются в зависимости от точности целым или дробным числом.
Изображение вариационного ряда графически в виде кривой, ординаты которой пропорциональны частотам, называется вариационной кривой (рис.1).
Вариационная кривая - очень удобный способ иллюстрации распределения признака, характеризующий его изменчивость в пределах совокупности.
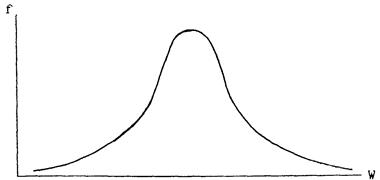
Рис. 1. Нормальная вариационная кривая, характеризующая
распределение признака
При большом числе определений вариационная кривая становится близкой к биноминальной кривой, хорошо соответствующей рядам разложения бинома (а + в),
(а + в) = а + в
(а + в)2 = а2+ 2ав + в2
(а + в)3 = а3+ За2в + Зав2+ в3
(а + в)4 = а4+ 4а3в + 6а2в2+ 4ав3+ в4
(а + в)5 = а5+ 5а4в + 10а3в2+ 10а2в3+ 5ав4+ в5 и так далее.
Коэффициенты этих разложений бинома дают так называемый арифметический треугольник Паскаля, который образует фигуру, соответствующую конфигурации вариационной кривой.
1 10 45 120 210 252 210 120 45 10 1
У биноминальных или "нормальных" кривых наибольшей частотой обладает средняя варианта, при удалении вправо и влево число вариант уменьшается. Кривая нормального распределения носит еще наименование кривой Гаусса.
Математические исследования биноминальной кривой широко применяются в вариационной статистике. На закономерностях нормального распределения основываются большинство методов статистической обработки экспериментальных данных, поскольку очень многие эмпирические распределения биологических признаков, характеризующихся непрерывной вариацией, в большей или меньшей степени следует нормальному распределению. Вероятно, первым, кто применил нормальное распределение для описания биологического материала, был Кетле. Позже Френсис Гальтон широко использовал кривую нормального распределения при статистическом исследовании наследственности.
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА. ЕЕ СВОЙСТВА
Основная величина, которая характеризует изучаемую совокупность, - это среднее значение признака. При обработке первичных экспериментальных материалов наиболее важным являются расчет средней арифметической величины. Предварительно необходимо рассмотрение основных свойств этого показателя.
Свойство I. Средняя арифметическая есть величина абстрактная.
Наиболее простой, но и наиболее трудоемкий метод - суммирование всех вариант и деление суммы на их число. Если каждая из 5 кур снесла 12-15-18-10-14 яиц, то
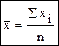 ,
,
то есть на несушку в среднем получено: 69 : 5 = 13,8 яиц. Разнородная группа показателей заменена одной цифрой. Хотя полученная дробная величина в действительности существовать не может, она используется в практической работе как величина отвлеченная, абстрактная. В более многочисленных выборках может применяться расчет взвешенной средней арифметической.
Приведенные выше в таблице 1 данные по яйценоскости кур удобно рассчитать следующим образом:
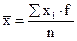 ;
; 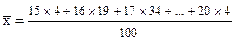 = 17,35 яйца.
= 17,35 яйца.
Получена дробная абстрактная величина, характеризующая изучаемую группу. Вместе с тем, средняя арифметическая величина конкретна, она выражается в тех же единицах измерения, что и варианты ряда. Средняя арифметическая характеризует всю совокупность в целом, а не отдельные ее члены. Она воспринимается как центр вариационного ряда.
Свойство II. Сумма центральных отклонений равна 0.
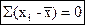
Это свойство удобно для проверки правильности расчета.
Средняя арифметическая является как бы точкой равновесия вариационного ряда, отклонения от которой как в отрицательную, так и в положительную сторону одинаковы, т. е. сумма положительных и отрицательных отклонений от центра равна 0. Если обозначить отклонение каждой варианты от средней арифметической через "а", расчет может быть проведен следующим образом:
| Таблица 2 | ||
| X | f | а |
| -2,35 | ||
| -1,35 | ||
| -0,35 | ||
| +0,65 | ||
| +1,65 | ||
| +2,65 |
|
 = 17, 35
= 17, 35
((-2,35)´ 4 + (-1,35)´ 19 + (-0,35) ´34)) = - 46,95
((+0,65)´ 28 + (+1,65) ´ 11 + (+2,65) ´4)) = + 46,95
Свойство III. Очень часто приходится вычислять среднюю арифметическую для групп в 100, 200, 1000 и более вариант. В такой группе трудно проводить суммирование и почти невозможно рассчитать индивидуальные отклонения. В этих случаях приходит на помощь свойство средней арифметической, выраженное такой формулой:
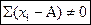
Сумма условных отклонений (отклонения от любого значения, не равного средней) не есть нуль.
В качестве примера рассмотрим ряд чисел: 1; 4; 5; 5; 5.
Пусть взятая наугад, принятая за условную среднюю величина А равна 5. В этом случае получим условные отклонения:
1-5=-4; 4-5=-1; 5-5= 0; 5-5= 0; 5-5= 0
å(xi - А) = -4 + -1 + 0 + 0 + 0 = -5.
На каждую дату приходится условное среднее отклонение

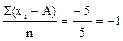 ;
;
 = 5 – 1= 4;
= 5 – 1= 4;  = 4;
= 4; 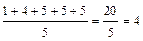 .
.
Если в этом примере взять А=2, результат будет тот же. Это свойство облегчает при больших выборках расчет средней не непосредственно, а через условную среднюю по формуле:
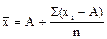 .
.
В качестве условных отклонений можно брать простые числа, а именно: 0, 1, 2, 3, 4, 5 и т.д. Это доказывается в следующем примере (табл. 3):
| Таблица 3 | |||
| xi | f | а | fa |
| Sa =100 | fa = 235 |
Если А = 15
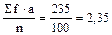
 = 15 + 2. 35 = 17,35 (т.е.
= 15 + 2. 35 = 17,35 (т.е.
то, что было получено
выше).
Этот расчет может быть
выражен формулой:
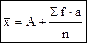
Обычно при обработке дискретного ряда за условную среднюю лучше брать величину, наиболее приближающуюся к средней арифметической. За такую величину принимается значение варианты с наибольшим количеством частот и расположенную в середине вариационного ряда. В данном случае А=17 (табл. 4).
Таблица 4
| xi | f | a | fa |
| -2 | -8 | ||
| -1 | -19 | ||
| +1 | +28 | ||
| +2 | +22 | ||
| +3 | +12 | ||
| Sfa = 35 |
{ -Sfa = -27
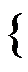
+Sfa = +52
 =А
=А 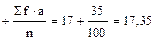 ;
;  =17,35 .
=17,35 .
Свойство IV. Если к каждому значению прибавить (или вычесть) постоянную величину (А), то средняя арифметическая из измененных вариант будет равна первоначальной средней, увеличенной (или уменьшенной) на ту же величину (А).
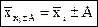
Каждая варианта предыдущего примера уменьшается на 10. Условная величина А=7 (табл.5):
Таблица 5
| xi | f | a | fa |
| -2 | -8 | ||
| -1 | -19 | ||
| +1 | +28 | ||
| +2 | +22 | ||
| +3 | +12 | ||
| Sfa = 35 |
 = 7
= 7 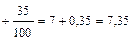
 = 7, 35.
= 7, 35.
В данном случае при сравнении с предыдущим примером ровно на 10 оказалась уменьшенной средняя арифметическая.
Это свойство удобно для упрощения расчета многозначных вариант в больших группах.
Свойство V. Если каждое значение умножить (или разделить) на постоянное число К, то средняя арифметическая из измененных вариант будет точно в К раз больше (или меньше) первоначальной средней:
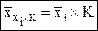 ;
; 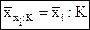
Практическое применение IV и V свойств средней арифметической имеет большое значение при преобразовании перед началом статистических расчетов исходных данных, представленных многозначными числами. В этих случаях расчеты осуществляются с простыми числами, и вся работа существенно упрощается. После выполнения расчетов полученные итоговые величины требуют восстановления, что проводится согласно следующим правилам:
1. Если при преобразовании все даты были разделены на одно и то же число К, то поправки, вносимые в конечные результаты, состоят в умножении величин  и S на К, а величин С и S2 на К2.
и S на К, а величин С и S2 на К2.
2. Если при преобразовании все даты умножены на число К, то поправки, вносимые в конечные результаты, обратные предыдущему случаю.
3. Если при преобразовании из всех значений дат вычитается (или прибавляется) одно и то же число А, то поправка, вносимая в конечные результаты, состоит только в сложении (или вычитании) величины А из величины  . Для значений С, S и
. Для значений С, S и 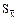 поправок не требуется.
поправок не требуется.
ВАРЬИРОВАНИЕ ПРИЗНАКОВ. ПОКАЗАТЕЛИ ВАРИАБЕЛЬНОСТИ
Значения признаков, составляющих совокупность, имеют различные величины. Различия иногда очень велики, иногда почти незаметны, однако имеются всегда, поскольку полной однородности внутри групп биологических объектов не бывает. Эта неоднородность вариант в совокупности называется разнообразием,варьированием или изменчивостью.
В биологии и, в частности в животноводстве, изменчивость признаков выражена очень сильно и имеет большое научное значение. Коровы в одном стаде различаются величиной удоев за лактацию, живой массой, процентом жира в молоке; овцы - настригами шерсти, длиной и тониной шерстного волокна, живой массой; куры-несушки - количеством яиц, снесенных в течение года, их массой и другими параметрами качества. Вариабельность признаков у животных является основой селекционного процесса, отбора и воспроизводства наиболее продуктивных особей. Вместе с тем, зооинженер постоянно стремится к наибольшей однородности стада животных, к снижению вариабельности признаков, поскольку однородное по продуктивности стадо может использоваться наиболее эффективно.
Отношение зооинженера к вариабельности признаков у животных не всегда однозначно, вариабельность в разных случаях может рассматриваться и как положительное, и как негативное явление. Но неизменно одно - вариабельность во всех случаях зоотехнической работы должна учитываться и измеряться. Важно знать и уметь рассчитывать показатели вариабельности признаков у животных.
Существенно также и то, что показатели вариабельности используются не только для непосредственного измерения вариабельности, но и для конструирования многих других статистических параметров. Биологическая или вариационная статистика является наукой, предназначенной для математических исследований биологических совокупностей на основе вариабельности составляющих их объектов.
Ниже в этом разделе рассматриваются основные показатели вариабельности признаков в биологических совокупностях.
Средняя арифметическая величина не может отразить этой вариабельности. При одном и том же среднем значении в двух разных совокупностях может быть неодинаковое разнообразие признаков. Это видно на простом примере.
Масса яиц в двух партиях и значения разнообразия следующие:
1) 45-48-52-54-56 Sxi = 255 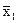 = 51
= 51
2) 43-50-50-52-60 Sxi = 255 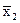 = 51
= 51
однако: 1) lim1 = 45-56
2) lim2 = 43-60,
т. е. разнообразие во второй группе больше. В данном случае разнообразие выражено в лимитах.
Лимиты - это наиболее простой показатель разнообразия. Они показывают размах значений (наивысший и наименьший уровни значений) и применяются достаточно широко. Однако лимиты не являются достаточно точным показателем и не всегда могут вскрыть все тонкости разнообразия в данной группе. Это определяет необходимость расчета более сложного показателя разнообразия признаков - среднего квадратического отклонения. Предположим, что в двух группах кур была получена следующая масса яиц (в граммах):
1) 44-46-47-48-50-54-56-57-58-59
lim = 44-59;  = 51,9; Sxi = 519; S = 5,53
= 51,9; Sxi = 519; S = 5,53
2) 44-52-52-52-52-52-52-52-52-59
lim = 44-59;  = 51,9; Sxi = 519; S = 3,58 .
= 51,9; Sxi = 519; S = 3,58 .
В этих группах средние арифметические и лимиты одинаковы, однако очевидно, что степень разнообразия в них совсем неодинакова. Уловить это разнообразие при помощи лимитов невозможно.
Для этого привлекается среднее квадратическое отклонение, которое в среднем характеризует отклонение каждой варианты от средней арифметической величины (табл. 6).
| Таблица 6 | |
| xi | xi - 
|
| -7,9 | |
| -5,9 | |
| -4,9 | |
| -3,9 | |
| -1,9 | |
| +2,1 | |
| +4,1 | |
| +5,1 | |
| +6,1 | |
| +7,1 |
S(xi -  );
);
(-7,9) + (-5,9) + (-4,9) + (-3,9) + (-1,9)
= - 24,5;
(+2,1) + (+4,1) + (+5,1) + (+6,1) + (+7,1)
= +24,5;
S(xi -  )= (-24,5) + (+24,5) = 0 .
)= (-24,5) + (+24,5) = 0 .
Поскольку сумма всех центральных отклонений равна нулю, для получения цифры, характеризующей эту изменчивость, каждое отклонение возводится в квадрат и получается их сумма, т.е. берется сумма квадратов цен-
тральных отклонений:S(xi -  )2.
)2.
Эта величина называется дисперсией, выражаемой через С.
|

Первое равенство - сумма квадратов центральных отклонений - S(xi -  )2 - определяет математическую сущность дисперсии.
)2 - определяет математическую сущность дисперсии.
Второе равенство, читаемое как сумма квадратов дат минус квадрат их суммы, деленный на объем выборки, - является производным первой формулы и имеет широкое применение как рабочая формула, удобная для расчета дисперсии (она может называться еще машинным алгоритмом дисперсии).
При расчете среднего квадратического отклонения необходимо отнести полученную величину дисперсии к числу дат минус единица и извлечь квадратный корень:
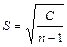 .
.
Как видно, чтобы определить удельную величину изменчивости, дисперсию делят на число дат, но не полное, а без единицы - (n - 1), что называется числом степеней свободы.
Число степеней свободы равно числу элементов свободного разнообразия, т. е. числу всех имеющихся элементов изучения без числа ограничений разнообразия. Сущность этого понятия может быть рассмотрена на следующем примере.
Если мы хотим взять для опыта три курицы без каких-либо условий отбора, то величина их продуктивности не имеет ограничений. Число степеней свободы в этом случае n = 3 - 0 = 3. Если же мы должны взять для опыта три курицы, обусловив заранее их среднюю продуктивность в группе, равную 200 яиц в год, то эта средняя величина является фактором, ограничивающим выбор. В этом случае первые две курицы могут иметь любую продуктивность, например, 150 и 210 или 180 и 190 яиц. Третья же курица тогда может иметь только одно значение продуктивности, а именно такое, при котором средняя продуктивность будет равна 200 яиц.
Если продуктивность двух первых куриц 150 и 210 яиц, то третьей -только 240 яиц:
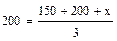 ; 600 = 150 + 210 + x;
; 600 = 150 + 210 + x;  = 600 - 150 - 210 = 240;
= 600 - 150 - 210 = 240;  = 240 яиц.
= 240 яиц.
При продуктивности двух первых кур 180-190 продуктивность третьей составит:
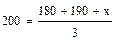 ; 600 = 180 + 190 + x;
; 600 = 180 + 190 + x;  = 600 - 180 – 190 = 230;
= 600 - 180 – 190 = 230;  = 230 яиц.
= 230 яиц.
В этих случаях два числа выбирать можно свободно, а третье не имеет свободы выбора Для этих трех чисел есть только две степени свободы: n = 3 - 1 = 2.
При вычислении средней арифметической никаких ограничений значения признака не имеется, поэтому число образующих ее элементов равно числу дат ( 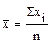 ).
).
При вычислении среднего квадратического отклонения имеется одно ограничение, оно рассчитывается для группы, имеющей определенную среднюю арифметическую величину. Поэтому разнообразие элементов, образующих среднее квадратическое отклонение, ограничено одним этим условием и n = n - 1.
При делении дисперсии на число степеней свободы получится величина, называемая девиатой, вариансой или средним квадратом:
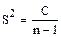 .
.
Извлечение квадратного корня из девиаты дает сигму, среднее квадратическое или стандартное отклонение:
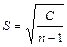 .
.
Расчет вышеуказанного примера может быть выполнен следующим образом (табл. 7):
Таблица 7
| n | xi | xi2 |
| Sxi=519 | S xi2=27211 |
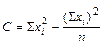 ;
; 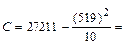 = 27211-26935,1 = 274,9
= 27211-26935,1 = 274,9
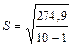 =
= 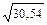 ; S = 5,53;
; S = 5,53;  = 51,9 .
= 51,9 .
То же самое можно получить путем оперирования с величиной отклонения от любого числа вариационного ряда (табл. 8).
| Таблица 8 | |||
| n | xi | D | D2 |
| SD=79 | SD2=899 |
Выбираем условную величину А равную 44.
Ведем расчет относительно наименьшей величины 44:
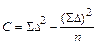 ;
;
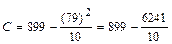
С = 899 – 624,1 = 274,9
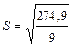 =
= 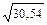 =5,5 .
=5,5 .
Среднее квадратическое отклонение служит основным показателем разнообразия значений признака в группе. Используется и как самостоятельный показатель, и как основа для конструирования многих других показателей: коэффициента вариации, ошибок репрезентативности, коэффициентов корреляции и регрессии, элементов дисперсионного анализа.
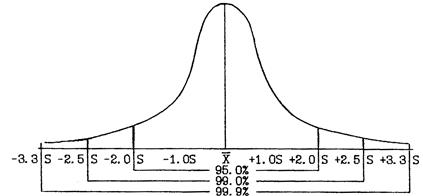
Рис 2. Квадратическое отклонение S как показатель и мера вариабельности признака
Среднее квадратическое отклонение - показатель именованный и выражается в тех же единицах, что и средняя арифметическая величина.
Практически стандартное отклонение может быть определено по размаху вариант в данном ряде. При числе дат в выборке от 30 до 200 в размахе укладывается 5S, при числе дат от 200 до 1000 - 6S, при числе дат более 1000 - 7S.
Можно сказать, что среднее квадратическое отклонение является мерой изменчивости в пределах данного вариационного ряда. Эта закономерность позволяет решить многие практические задачи, что рассматривается в последующих разделах настоящего пособия.
Среднее квадратическое отклонение служит хорошим показателем выражения разнообразия при соблюдении следующих условий.
1. Если сравнивается разнообразие в разных вариационных рядах, но по аналогичному признаку.
Например: масса яйца: 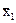 = 55,3 S1 = 4,06
= 55,3 S1 = 4,06
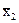 = 54,3 S2 = 3,93
= 54,3 S2 = 3,93
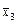 = 58,6 S3 = 3,71.
= 58,6 S3 = 3,71.
2. Если математические выражения средних величин сравниваемых показателей обозначаются числами одного порядка (яйценоскость, число пор в скорлупе, удой за лактацию, многоплодие и т.п.).
При отсутствии этих условий среднее квадратическое отклонение не дает возможности сравнить разнообразие в выборках разных показателей.
| Например: | масса яйца | - | S = 4,06 г |
| индекс формы яйца | - | S = 0,059 | |
| толщина скорлупы | - | S = 0,034 мм | |
| число пор в скорлупе | - | S = 25,3 пор | |
| индекс белка | - | S = 0,028 ед. | |
| единицы Хау | - | S = 6,04 | |
| индекс желтка | - | S = 0,041 |
По этим величинам нельзя установить, какой из показателей качества яйца отличается большим разнообразием, так как эти показатели несравнимы.
Для возможности сравнения такого разнообразия применяется особый, относительный показатель - коэффициент вариабельности, выражающий величину среднего квадратического отклонения по отношению к средней арифметической в процентах:
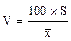 .
.
При расчете коэффициента вариабельности (V) вышеприведенный пример выглядит следующим образом:
Дата добавления: 2020-10-25; просмотров: 681; |

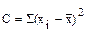 ; или
; или