Сложение гармонических колебаний. Метод векторных диаграмм

Гармоническое колебание x = a Cos (wt + a) геометрически может быть представлено проекцией на произвольное направление x вектора 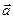, вращающегося вокруг неподвижной оси с угловой скоростью w. Длина этого вектора равна амплитуде колебания, а его первоначальное направление образует с осью x угол, равный начальной фазе колебания — a. Используя это геометрическое толкование, решим задачу о сложении двух гармонических колебаний одинаковой частоты и направления.

x = x₁ + x₂ = a₁Cos (wt + a₁) + a₂ Cos (wt + a₂).

Построим вектор 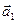(под углом a₁ к оси x), изображающий первое колебание. Прибавим к нему векторно вектор 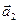, образующий угол a₂ с осью x (рис. 12.8). Сумма проекций этих векторов на ось x равна проекции на эту ось вектора 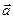, равного сумме 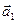и .

= +

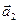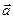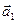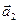
x = x₁ + x₂.

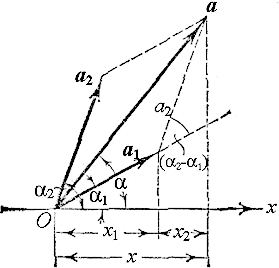
Рис. 12.8

Приведем эту векторную диаграмму во вращение с угловой скоростью w вокруг оси, проходящей через начало координат — точку О. При этом равенство x = x₁ + x₂ сохранится неизменным во времени, хотя сами проекции x, x₁ и x₂ будут теперь пульсировать по гармоническому закону с одинаковой частотой w и с начальными фазами a, a₁ и a₂ — соответственно. В результате сложения двух колебаний:

x₁ = a₁ Cos (wt + a₁) и x₂= a₂ Cos (wt + a₂) возникает новое колебание x = x₁ + x₂ =

= a Cos (wt + a), частота которого — w – совпадает с частотой складываемых колебаний. Его амплитуда равна модулю вектора 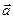, а начальная фаза a, как следует из рис. 12.8, равна:

.

Для подсчета амплитуды «а» суммарного колебания, воспользуемся теоремой косинусов:

.

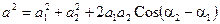Величина амплитуды результирующего колебания зависит не только от амплитуд складываемых колебаний а₁ и а₂, но и от разности их начальных фаз. Колебание с максимальной амплитудой, а = a_max = a₁ + a₂ возникает при сложении синфазных колебаний, то есть когда их начальные фазы совпадают: a₁ = a₂.

Если разность фаз (a₂ – a₁) = p, то амплитуда суммарного колебания будет минимальной a = a_min = |a₁ – a₂|. Если амплитуды таких колебаний, происходящих в противофазе, равны (a₁ = a₂), то амплитуда суммарного колебания окажется равной нулю.

Этим методом векторных диаграмм нам предстоит в будущем часто пользоваться при сложении не только колебаний, но и волн.