Пружинный осциллятор

Пружинный маятник — это грузик массой m, прикреплённый к пружине жесткостью k. Грузик может двигаться вдоль оси x по горизонтальной поверхности без трения (рис. 12.4). Начало отсчета совместим с положением равновесия. Тогда координата грузика — x в любой момент времени равна деформации пружины. На движение маятника оказывает влияние только упругая сила. Запишем уравнение движения этого маятника.

Рис. 12.4

.

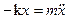Это дифференциальное уравнение собственных незатухающих колебаний пружинного осциллятора. Его принято записывать так:

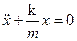(12.3)

Решением этого уравнения является гармоническая функция

x = a Cos (w₀t + a). (12.4)

Покажем, что предлагаемая функция удовлетворяет уравнению (12.3). Возьмём вторую производную по времени функции (12.4)

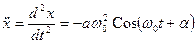. (12.5)

Подставим (12.4) и (12.5) в дифференциальное уравнение (12.3).

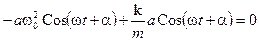
Это равенство становится тождеством, если .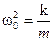

Так мы показали, что пружинный маятник при отсутствии сил трения совершает собственные незатухающие гармонические колебания x = aCos(w₀t + a) c частотой 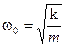. Эта частота зависит только от свойств осциллятора: массы груза m и жёсткости пружины k.

Начальная фаза — a определяется методом задания колебаний. Оттянем вначале груз на расстояние x₀ = a и отпустим. При таком запуске колебаний в момент t = 0, x(0) = x₀ = a. При этом Cos (wt + a) = Cos a = 1. Откуда следует, что a = 0.

Теперь запустим колебания по–другому. Нанесем по грузику, покоящемся в положении равновесия, короткий удар, сообщив ему тем самым начальную скорость v₀. В начальный момент времени t = 0, x(0) = 0 и Cos (wt + a) = Cos a = 0. Отсюда приходим к выводу, что при таком запуске колебаний a = 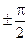. Знак начальной фазы в этом случае определяется направлением начальной скорости v₀.

Можно оттянуть грузик из положения равновесия и не просто отпустить, но и толкнуть. Тогда начальная фаза может принять любое значение от 0 до 2p.

Зная частоту колебаний 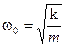, легко вычислить период:

.

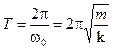Скорость колеблющегося грузика:

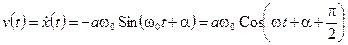(12.6)

тоже меняется по гармоническому закону с частотой w₀. Амплитуда колебания скорости равна aw₀, а по фазе скорость на 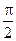опережает смещение.

Ускорение груза

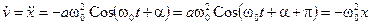(12.7)

колеблется с той же частотой w₀, опережая смещение по фазе на p (рис. 12.5).

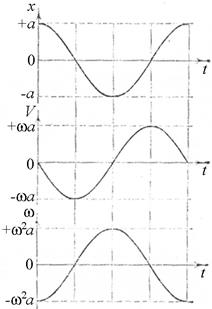
Рис. 12.5