Движение тел переменной массы. Реактивное движение

До сих пор мы считали, что масса тел в процессе их движения не меняется. Но так обстоит дело не всегда.

Рассмотрим, например, движение ракеты — классический пример тела, масса которого уменьшается по мере расхода топлива (рис. 4.4).

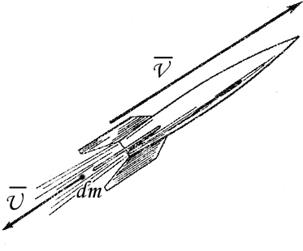
Рис. 4.4

Пусть в момент времени t масса ракеты m, а её скорость 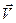. Спустя dt секунд скорость ракеты увеличится на 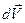, а масса уменьшится на величину dm и станет (m – dm).

dm — масса сгоревшего топлива, которое покинуло ракету со скоростью 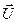относительно неё. Изменение импульса системы за время dt можно представить в следующем виде:

.

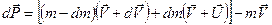Слагаемым dm∙dV пренебрежем как малой величиной высшего порядка по сравнению с остальными слагаемыми. Значит

.

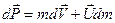Это изменение импульса системы равняется импульсу действующей внешней силы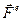

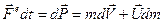
Полученный результат перепишем в форме уравнения движения

(4.14)

Здесь: слева — произведение массы ракеты на её ускорение,

справа — действующие силы: 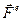— внешняя сила,

— реактивная сила.

Реактивная сила возникает потому, что вылетающим продуктам сгорания сообщается относительная скорость 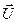. Вначале топливо было в покое относительно ракеты. Затем оно двигалось ускоренно и достигло скорости 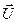. Это ускорение обусловлено силой взаимодействия продуктов сгорания с ракетой. Но по третьему закону Ньютона сила действует не только на продукты сгорания, но и на ракету. Это и есть реактивная сила, пропорциональная относительной скорости 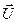и секундному расходу топлива .

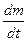Уравнение (4.14) называется уравнением движением тела переменной массы. Оно было впервые получено И.В. Мещереным и носит его имя:

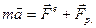(4.15)

где: — реактивная сила.

Теперь посмотрим, как будет двигаться ракета, на которую не действуют никакие внешние силы ( 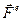= 0). Движение ракеты будем считать прямолинейным и спроецируем уравнение (4.15) на направление её движения:

;

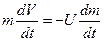отсюда:

;

или

. (4.16)

Постоянную интегрирования с найдём из начального условия. Будем считать, что в начальный момент полета — в момент старта — скорость ракеты V₍₀₎ = 0, а её масса равна стартовому значению m₀.

Перепишем (4.16) для этих начальных условий:

V₍₀₎ = 0 = —U∙ln∙m₀ + c,

то есть

c = U∙ln∙m₀

Используя этот результат в уравнении (4.16) получим

. (4.17)

Это соотношение называется формулой Циолковского.

Используя эту формулу, оценим, например, какой должна быть стартовая масса ракеты m₀, чтобы вывести на околоземную орбиту груз массой m = 10³ кг.

Первая космическая скорость составляет V = 8 км/с, а относительная скорость истечения продуктов сгорания U — порядка 2 км/с.

Тогда

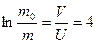
и

кг.

Если скорость истечения U принять равной 1 км/с, то есть вдвое меньше, то стартовая масса ракеты возрастёт до значения 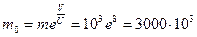кг.

То есть 3 тысячи тонн!

Таково влияние качества ракетного топлива на стартовую массу ракеты.