С ожиданием (СМО с конечной очередью)

Этому графу состояний соответствует система дифференциальных уравнений для вероятностей состояний, которую обычно интегрируют для начальных условий

Р₀ (0) = 1, Р_i (0) = 0 (i ¹ 0),

т.е. в момент времени t = 0 система свободна от заявок. Для стационарного режима работы СМО с ожиданием, когда l = const, m = const, m < ¥, t ® ¥, используя результаты главы 3, имеем

,

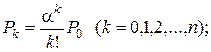
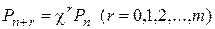где

; .

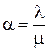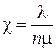Используя нормировочное условие

,

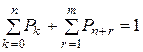получим

;

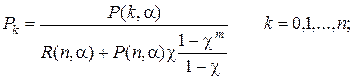
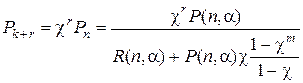где

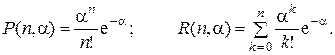
Для сокращения дальнейших записей введем обозначения:

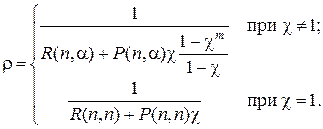(4.1)

Заметим, что если нормировочное условие записать в виде

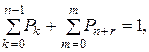
то величина r будет определяться так:

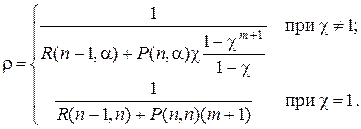(4.2)

Из (4.1) и (4.2) вытекают следующие равенства:

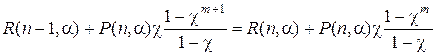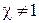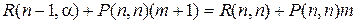при ;

при ,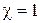

в справедливости которых для любых положительных a и c и любых положительных целых n и m легко убедиться.

С одной стороны,вероятность обслуживания заявки равна вероятности того, что заявка, поступившая на обслуживание, застает свободным хотя бы один из каналов или хотя бы одно место в очереди:

.

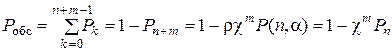С другой стороны,

,

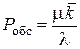где 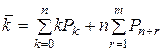– среднее число занятых каналов.

Следовательно,

.

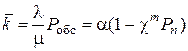Вероятность того, что канал занят,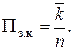

Вероятность того, что система полностью загружена ( 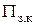), равна вероятности того, что в системе заняты все каналы:

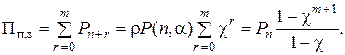
Среднее время неполной загрузки ( 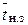) СМО с ожиданием определяется как

Среднее время полной загрузки ( ) с учетом эргодического свойства определяется следующим соотношением:

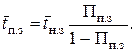
Среднее время наличия очереди ( ) (т.е. время нахождения системы в группе макросостояний 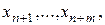см. рис. 4.1) рассчитывается по формуле

.

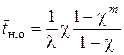При нахождении среднего времени занятости канала ( 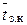) рассуждаем следующим образом. Допустим, что к моменту окончания обслуживания заявки в рассматриваемом канале очереди нет. Вероятность этой гипотезы 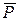_н.о = 1 –Р_н.о, где Р_н.о – вероятность наличия очереди в системе.

Если в системе нет очереди к моменту окончания обслуживания, то среднее время занятости канала будет равно 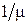. Если к моменту окончания обслуживания в системе будет очередь (вероятность этой гипотезы Р_н.о), то среднее время занятости канала будет равно 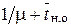. Применяя формулу полного математического ожидания, можно найти среднее время занятости канала:

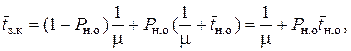
и вероятность наличия очереди:

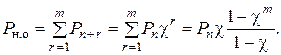
Среднее время простоя канала:

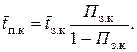
При необходимости можно определить и другие характеристики системы (см., например, работу [9]).