Вычисление дискретных логарифмов в конечной группе

Криптографы интересуются дискретными логарифмами следующих трех групп:

— Мультипликативная группа полей простых чисел: GF(p)

— Мультипликативная группа конечных полей степеней 2: GF(2ⁿ)

— Группы эллиптической кривой над конечными полями F: EC(F)

Безопасность многих алгоритмов с открытыми ключами основана на задаче поиска дискретных логарифмов, поэтому эта задача была глубоко изучена. Хороший подробный обзор этой проблемы и ее наилучшие решения на соответствующий момент времени можно найти в [1189, 1039]. Лучшей современной статьей на эту тему является [934].

Если p является простым числом и используется в качестве модуля, то сложность поиска дискретных логарифмов в GF(p) по существу соответствует разложению на множители числа n того же размера, где n - это произведение двух простых чисел приблизительно равной длины [1378,934]. То есть:

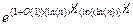
Решето числового поля быстрее, оценка его эвристического времени выполнения:

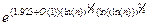
Стивен Полиг (Stephen Pohlig) и Мартин Хеллман нашли способ быстрого вычисления дискретных логарифмов в GF(p) при условии, что p - 1 раскладывается на малые простые множители [1253]. По этой причине в криптографии используются только такие поля, для которых p - 1 обладает хотя бы одним большим простым множителем. Другой алгоритм [14] вычисляет дискретных логарифм со скоростью, сравнимой с разложением на множители, он был расширен на поля вида GF(pⁿ) [716]. Этот алгоритм был подвергнут критике в [727] по ряду теоретических моментов. В других статьях [1588] можно увидеть, насколько на самом деле трудна проблема в целом.

Вычисление дискретных логарифмов тесно связано с разложением на множители. Если вы можете решить проблему дискретного логарифма, то вы можете и разложить на множители. (Истинность обратного никогда не была доказана.) В настоящее время существует три метода вычисления дискретных логарифмов в поле простого числа [370, 934, 648]: линейное решето, схема целых чисел Гаусса и решето числового поля.

Предварительное, объемное вычисление для поля должно быть выполнено только один раз. Затем, быстро можно вычислять отдельные логарифмы. Это может серьезно уменьшить безопасность систем, основанных на таких полях. Важно, чтобы различные приложения использовали различные поля простых чисел. Хотя несколько пользователей одного приложения могут применять общее поле.

В мире расширенных полей исследователями не игнорируются и GF(2ⁿ). Алгоритм был предложен в [727]. Алгоритм Копперсмита (Coppersmith) позволяет за приемлемое время находить дискретные логарифмы в таких полях как GF(2¹²⁷) и делает принципиально возможным их поиск в полях порядка GF(2⁴⁰⁰) [368]. В его основе лежит [180]. У этого алгоритма очень велика стадия предварительных вычислений, но во всем остальном он хорош и эффективен. Реализация менее эффективной версии этого же алгоритма после семи часов предварительных вычислений тратила на нахождение каждого дискретного логарифма в поле GF(2¹²⁷) лишь несколько секунд [1130, 180]. (Это конкретное поле, когда-то использовавшееся в некоторых криптосистемах [142, 1631, 1632], не является безопасным.) Обзор некоторых из этих результатов можно найти в [1189, 1039].

Позднее были выполнены предварительные вычисления для полей GF(2²²⁷), GF(2³¹³) и GF(2⁴⁰¹), удалось значительно продвинуться и для поля GF(2⁵⁰³). Эти вычисления проводились на nCube-2, массивном параллельном компьютере с 1024 процессорами [649, 650]. Вычисление дискретных логарифмов в поле GF(2⁵⁹³) все еще находится за пределами возможного.

Как и для нахождения дискретных логарифмов в поле простого числа, для вычисления дискретных логарифмов в полиномиальном поле также требуется один раз выполнить предварительные вычисления. Тахер Эль-Джамаль (Taher EIGamal) [520] приводит алгоритм вычисления дискретных логарифмов в поле GF(p²).