Где коэффициент s, с учетом (4.12), имеет вид

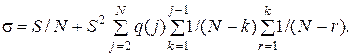(4.15)

Здесь S определяется равенством (4.13), а f(x), следовательно, имеет экспоненциальный вид:

.

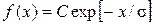Таким образом, асимптотическое распределение P(x, k, m) вектора 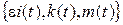, где e определяется равенством (4.14а), с учетом решения первого этапа имеет вид

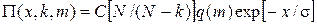. (4.16)

Константа С определяется условием нормировки:

,

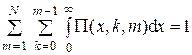и имеет вид

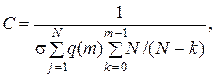
здесь s определяется равенством (4.15).

Распределение (4.16) решает задачу исследования математической модели СМО с буфером бесконечной длины и позволяет находить основные вероятностные характеристики. Рассмотрим нахождение некоторых из них:

1. Распределение числа свободных приборов (обслуживающих)

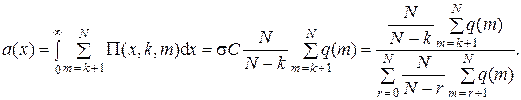
2. Предельное значение коэффициента загрузки приборов

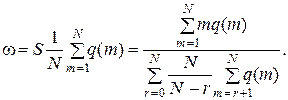
3. Асимптотическое распределение числа заявок в очереди (экспоненциальное распределение) с плотностью (4.15), имеет смысл среднего значения. Поэтому среднее число заявок в буфере .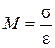

4. Средняя величина задержки (время очереди) 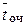в буфере определяется по формуле Литтла:

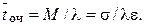
5. Пропускная способность S СМО с буфером определяется равенством (4.13).

Аналогично можно определить и другие вероятностные характеристики СМО с буфером.

Таким образом, выше рассмотрена и построена векторная СМО с бесконечной очередью и однородными запросами на число мест в очереди. Получены явные выражения для расчета основных вероятностных характеристик СМО с буфером.