Системы массового обслуживания с отказами и частичной взаимопомощью между каналами
Постановка задачи. На вход n-канальной СМО поступает простейший поток заявок с плотностью λ. Плотность простейшего потока обслуживания каждого канала равна μ. Если поступившая на обслуживание заявка застает все каналы свободными, то она принимается на обслуживание и обслуживается одновременно l каналами (l < n). При этом поток обслуживаний одной заявки будет иметь интенсивность lm.
Если поступившая на обслуживание заявка застает в системе одну заявку, то при n ≥ 2l вновь прибывшая заявка будет принята к обслуживанию и будет обслуживаться одновременно l каналами.
Если поступившая на обслуживание заявка застает в системе i заявок (i = 0,1, ... ), при этом (i + 1)l ≤ n, то поступившая заявка будет обслуживаться l каналами с общей производительностью lm. Если вновь поступившая заявка застает в системе j заявок и при этом выполняются совместно два неравенства: (j + 1)l > n и j < n, то заявка будет принята на обслуживание. В этом случае часть заявок может обслуживаться l каналами, другая часть меньшим, чем l, числом каналов, но в обслуживании будут заняты все n каналов, которые распределены между заявками произвольным образом. Если вновь поступившая заявка застанет в системе n заявок, то она получает отказ и не будут обслуживаться. Попавшая на обслуживание заявка обслуживается до конца (заявки «терпеливые»).
 |
Граф состояний такой системы показан на рис. 3.8.
Рис. 3.8. Граф состояний СМО с отказами и частичной
взаимопомощью между каналами
Заметим, что граф состояний системы до состояния xh с точностью до обозначений параметров потоков совпадает с графом состояний классической системы массового обслуживания с отказами, изображенным на рис. 3.6.
Следовательно,
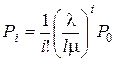 (i = 0, 1, ..., h).
(i = 0, 1, ..., h).
Граф состояний системы, начиная от состояния xh и кончая состоянием xn, совпадает с точностью до обозначений с графом состояний СМО с полной взаимопомощью, изображенным на рис. 3.7. Таким образом,
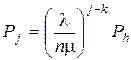 .
.
Введем обозначения λ / lμ = ρl ; λ / nμ = χ, тогда
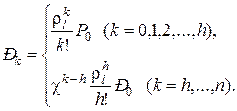
С учетом нормированного условия получаем
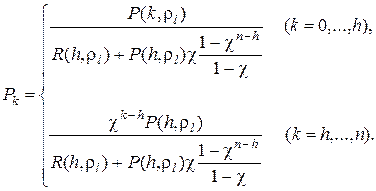
Дата добавления: 2021-01-11; просмотров: 626;











