Векторная модель с конечной очередью и неоднородными запросами на число мест в очереди
Постановка задачи. На вход СМО, содержащей N обслуживающих приборов и L мест в очереди, поступает неоднородный входной поток с интенсивностью l. Для определенности будем работать в рамках СМО с ограниченной очередью. При этом характеристики модели будут аналогичны представленным в главе 3. Отличие состоит в следующем.
На обслуживании в СМО может находиться произвольное число заявок, пока не будет исчерпан ресурс, и еще L заявок будет в очереди. Заявки, которые не могут быть приняты немедленно на обслуживание или поставлены в очередь на обслуживание, получают отказ в обслуживании и покидают систему. По окончании процесса обслуживания одной из заявок освобождающиеся приборы вместе с другими свободными приступают к обслуживанию заявки, стоящей на первом месте очереди, или ожидают прихода следующей заявки, если очередь пуста.
На основании изложенного была разработана имитационная статистическая модель (МСО). В качестве аналитической модели (ВМО) с ограниченной очередью предлагается следующая [11]. Описание входного потока соответствует приведенному в главе 3. Состояние ВМО представим в виде вектора:
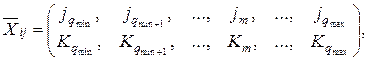
где jm – количество заявок в очереди, требующих для своего обслуживания m приборов; Km – количество заявок в системе, каждая из которых обслуживается m приборами; 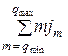 – количество заявок, находящихся в очереди;
– количество заявок, находящихся в очереди; 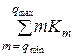 – количество заявок в системе, находящихся на обслуживании.
– количество заявок в системе, находящихся на обслуживании.
Тогда число свободных ( 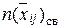 ) и занятых (
) и занятых ( 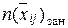 ) приборов в системе определяется как:
) приборов в системе определяется как:
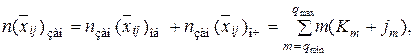
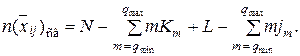
Из состояния 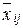 система может перейти в любое другое состояние
система может перейти в любое другое состояние 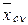 . Так как в системе действует l входных потоков (l = qmax – qmin+ 1), то из состояния
. Так как в системе действует l входных потоков (l = qmax – qmin+ 1), то из состояния 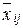 потенциально возможны l прямых переходов. Однако из-за ограниченности ресурсов (N и L) не все эти переходы осуществимы. Пусть ВМО находится в состоянии
потенциально возможны l прямых переходов. Однако из-за ограниченности ресурсов (N и L) не все эти переходы осуществимы. Пусть ВМО находится в состоянии 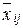 , и приходит заявка, требующая m приборов. Если m £ nсв(
, и приходит заявка, требующая m приборов. Если m £ nсв( 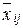 )об, то заявка принимается на обслуживание и система переходит в состояние
)об, то заявка принимается на обслуживание и система переходит в состояние 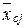 с интенсивностью lm, причем
с интенсивностью lm, причем
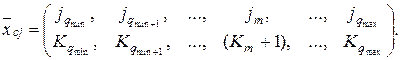
Если же заявка затребует приборов больше, чем имеется свободных, то она встает в очередь при условии, что m £ nсв( 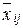 )оч, т.е.
)оч, т.е.
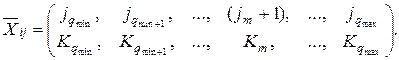
Если же места и в очереди заняты, то заявка получает отказ, а СМО остается в состоянии 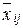 . Интенсивности обслуживания аналогичны описанным в главе 3.
. Интенсивности обслуживания аналогичны описанным в главе 3.
При завершении обслуживания одной из заявок система перейдет в состояние, в котором соответствующая координата имеет значение на единицу меньше, чем в состоянии 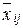 , т.е.
, т.е.
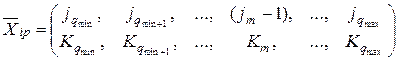 ,
,
произойдет обратный переход.
На рис. 4.2 представлен пример фрагмента графа ВМО для n = 3, q = = 1–3, P(m) = 1/3, L = 3.

Рис. 4.2. Фрагмент графа переходов ВМО СМО
По графу состояний с нанесенными интенсивностями переходов составляется система алгебраических уравнений, из решения которой находятся вероятности P( 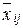 ), а по последним определяются характеристики СМО. Рассмотрим нахождение Ротк и tоч.
), а по последним определяются характеристики СМО. Рассмотрим нахождение Ротк и tоч.
На основании сведений, изложенных в главе 3, и особенностей ВМО получим, что
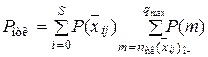 . (4.3)
. (4.3)
Определим tоч. Допустим, что время ожидания начала обслуживания данной заявки попало в элементарный интервал (t, t + dt). Вероятность этой гипотезы приближенно равна fоч(t)dt, где fоч(t) – плотность распределения вероятности времени пребывания заявки в очереди. За время пребывания в очереди за этой заявкой образуется очередь, в которой в среднем будет находиться lt заявок. Следовательно, математическое ожидание числа заявок (r), находящихся в очереди, будет определяться по выражению:
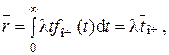
где 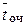 – среднее время ожидания заявки в очереди. Отсюда
– среднее время ожидания заявки в очереди. Отсюда
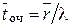 . (4.4)
. (4.4)
В свою очередь,
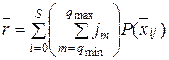 . (4.5)
. (4.5)
Тогда на основании (4.4) и (4.5) получим
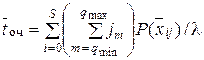 .
.
В табл. 4.1 приведены расчетные значения Ротк и 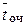 при r = l/m = = 0,6; N = 1–2, L = 1–2 для моделей СМО и ВМО.
при r = l/m = = 0,6; N = 1–2, L = 1–2 для моделей СМО и ВМО.
Таблица 4.1
| N, L | Pотн ВМО | Pотн МСО | 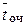 ВМО × 10-2 ВМО × 10-2
| 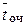 МСО × 10-2 МСО × 10-2
|
| 1,1 | 0,1836 | 0,1849 | 3,06 | 3,09 |
| 1,2 | 0,0993 | 0,1050 | 6,61 | 6,58 |
| 2,1 | 0,0294 | 0,0301 | 0,50 | 0,47 |
| 2,2 | 0,0249 | 0,0234 | 2,20 | 2,21 |
Проверка адекватности моделей (ВМО и СМО) проводилась на основании критерия Уилкоксона [25], который показал совпадение с точностью не хуже 2 %.
Итак, следует отметить, что предложенная в данном разделе ВМО позволяет рассчитывать характеристики СМО с запросами на случайное число обслуживающих приборов и мест в очереди. Практическая возможность использования ВМО связана с применением пакетов прикладных программ для расчета системы алгебраических уравнений.
Дата добавления: 2021-01-11; просмотров: 670;











