Интеграл Лебега на множестве конечной меры.
Пусть задано (X,S,m) – пространство с конечной мерой и f : X®R измеримая функция.
Определение. Назовём функцию f интегрируемой (суммируемой) на X, если существует последовательность простых интегрируемых на X функций 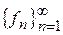 , сходящаяся равномерно к f. Интегралом Лебега функции f на множестве X называется предел интегралов от функций
, сходящаяся равномерно к f. Интегралом Лебега функции f на множестве X называется предел интегралов от функций 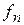 :
:
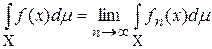 .
.
Различие в определениях интеграла Римана и интеграла Лебега заключается в том, что при составлении интегральных сумм Римана разбиение производится по признаку близости точек на оси OX, а при составлении интегральных сумм Лебега – по признаку близости значений функции.
Основные свойства интеграла Лебега по множеству конечной меры:
1) для любого измеримого множества 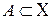
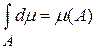 ;
;
2) если 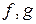 – интегрируемы по Лебегу, то функция
– интегрируемы по Лебегу, то функция 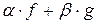 , где
, где 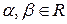 , интегрируема по Лебегу и справедливо равенство
, интегрируема по Лебегу и справедливо равенство
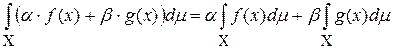 ;
;
3) если f – измеримая ограниченная функция, то она интегрируема по Лебегу;
4) если f – интегрируемая функция и 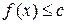 , то
, то
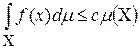 ;
;
5) если f – интегрируемая функция и 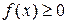 , то
, то
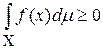 ;
;
6) если 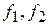 – интегрируемые функции и
– интегрируемые функции и 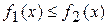 , то
, то
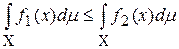 ;
;
7) если 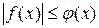 , где
, где 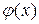 – интегрируемая, а
– интегрируемая, а 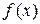 – измеримая, то f интегрируема по Лебегу;
– измеримая, то f интегрируема по Лебегу;
8) если 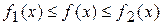 , где
, где 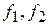 – интегрируемые, а f – измеримая функция, то f – интегрируема.
– интегрируемые, а f – измеримая функция, то f – интегрируема.
9) если f – интегрируемая функция, а g – ограниченная 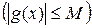 измеримая функция, то
измеримая функция, то 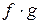 – интегрируема, причём
– интегрируема, причём
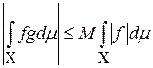 .
.
10) если f интегрируема на X, то f интегрируема на любом измеримом подмножестве из X и
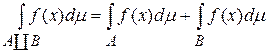 ,
,
(это свойство называется аддитивностью интеграла Лебега);
11) функции f и 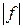 интегрируемы или неинтегрируемы одновременно, причём справедлива оценка
интегрируемы или неинтегрируемы одновременно, причём справедлива оценка
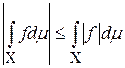 ;
;
12) если 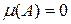 , то
, то 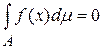 ;
;
13) если 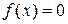 почти всюду на X, то
почти всюду на X, то 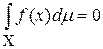 ;
;
14) если 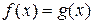 почти всюду, то
почти всюду, то 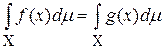 ;
;
15) если 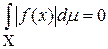 , то
, то 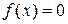 почти всюду на X.
почти всюду на X.
3. Абсолютная непрерывность и σ-аддитивность интеграла Лебега
Теорема 1 (абсолютная непрерывность интеграла Лебега).
Пусть 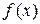 – интегрируемая на множестве A функция. Тогда для всех
– интегрируемая на множестве A функция. Тогда для всех 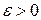 существует
существует 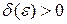 , что
, что 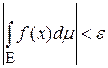 для всякого измеримого множества
для всякого измеримого множества 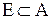 такого, что
такого, что 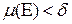 .
.
Теорема 2 (σ-аддитивность интеграла Лебега).
Пусть f – измеримая функция по множеству A и пусть 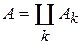 ,
, 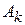 – измеримые множества. Тогда f интегрируема по каждому
– измеримые множества. Тогда f интегрируема по каждому 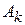 и
и 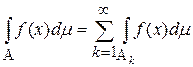 , причём ряд сходится абсолютно.
, причём ряд сходится абсолютно.
Теорема 3.Если 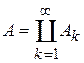 , f интегрируема на каждом
, f интегрируема на каждом 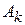 и ряд
и ряд 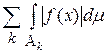 сходится, то функция f интегрируема на A и
сходится, то функция f интегрируема на A и 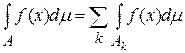 .
.
Дата добавления: 2021-07-22; просмотров: 527;











