Матрица перехода имеет вид

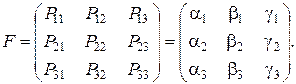
После первого испытания вероятности состояний равны:

(P₁(1); P₂(1); P₃(1)) = (P₁(0); P₂(0); P₃(0))×F = a₁P₁(0) a₂P₂(0) + a₃P₃(0);

b₁P₁(0) + b₂P₂(0) + b₃P₃(0); g₁P₁(0)+g₂P₂(0)+g₃P₃(0).

На рис. 2.4 представлен граф возможных переходов с соответствующими вероятностями.

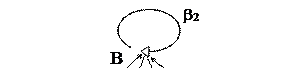
Рис. 2.4. Граф перехода к примеру 2.3

Например,

P₂(1) = 1/3{(a₁ + a₂ + a₃) b₁ + (b₁ + b₂ + b₃) b₂ + (g₁ + g₂ + g₃) b₃}.

Предположим, что результатом i-го испытания является состояние А; посмотрим, какова в этом случае вероятность перейти в состояние А в (i+2)-м испытании. Рассматривая i-е испытание как начальное, имеем

(P₁(2); P₂(2); P₃(2)) = (1; 0; 0) F² = (a₁² + b₁a₂ + g₁a₃;

a₁b₁ + b₁b₂ + g₁b₃; a₁ g₁ + b₁g₁ + g₁g₃).

Следовательно,

.

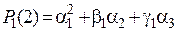Пример 2.4. Эскадрилья бомбардировщиков [13] насчитывает 4 самолета. Как правило, эскадрилья получает боевое задание один раз в день. Если к концу дня наличный состав уменьшается до 0; 1 или 2 самолетов из-за потерь, нанесенных противником, командир эскадрильи получает 1 самолет из резерва; этот самолет ему доставляют ночью. Если наличный состав остается равным 3 или 4 самолетам, то командир не имеет права на пополнение. На следующий день, если в наличии имеется 3 или 4 самолета, задание эскадрилье дается, в противном случае задание отменяется. Во время выполнения задания каждый самолет может быть выведен из строя с вероятностью Р.

Если на задание посылается n самолетов, вероятность того, что k из них будут выведены из строя, задается биномиальным распределением

.

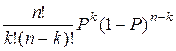Граф переходов показан на рис. 2.5; здесь имеется цепь Маркова с матрицей

в момент i +1

где q = 1 –p

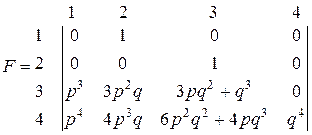
Рис. 2.5. Граф перехода к примеру 2.4

Первая строка матрицы относится к случаю, когда в момент i имеется один самолет; тогда в момент i+1 в наличии будут два самолета, потому что будет получено пополнение (1 самолет) и не будет вылета на задание. Вторая строка представляет состояние 2 (2 самолета) в момент i; в этом случае также не будет вылета и будет пополнение. Третья строка изображает состояние 3 в момент i; очевидно, в этом случае состоится боевой вылет группы в составе 3 самолетов; вероятность того, что к моменту i+1 будет 1 самолет, соответствуют случаю, когда ни один самолет не вернется, следовательно, р₃₁ = р³; вероятность того, что к моменту i+1 будет 2 самолета, соответствует случаю, когда с задания вернется 1 самолет, т.е. p₃₂ = = 3p²q; вероятность того, что в момент i = 1 будет 3 самолета, соответствует случаю возвращения 2 или 3 самолетов, откуда p₃₃ = 3pq² + q³. Аналогичными рассуждениями можно найти элементы четвертой строки рассматриваемой матрицы.