С учетом ранее введенных определений

P₁(t) = lt + 0(t); P₀(t) = 1 – lt + 0(t). (2.5)

Подставим в систему уравнений (2.4) полученные значения вероятностей P₁(t) и P₀(t). Затем, перенеся в левую часть уравнений P_k(t), поделим левые и правые части уравнения на t. Переходя к пределу, получим

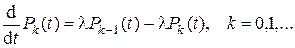(2.6)

Решив систему дифференциальных уравнений, получим формулу Пуассона

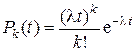. (2.7)

Таким образом, вероятность поступления точно k заявок простейшего потока за отрезок времени t определяется формулой Пуассона (2.7). По этой причине простейший поток также называют стационарным пуассоновским потоком.

Основные характеристики простейшего потока.При объединении n независимых простейших потоков c l₁, l₂, …, l_n образуется простейший поток с параметром l₁ + l₂ + … + l_n. Вероятность точно k заявок за отрезок времени t определяется формулой Пуассона

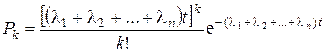. (2.8)

Можно показать, что объединение большого числа независимых стационарных ординарных потоков с практически любым последействием при малых значениях параметров этих потоков создает общий поток, близкий к простейшему. Если каждый из потоков поступает от отдельного источника заявок, то простейший поток можно представить как поток от бесконечного числа источников, параметры каждого из которых стремятся к нулю.

Сумма вероятностей всех возможных значений числа поступающих заявок за рассматриваемый промежуток времени t равна 1. Действительно,

.

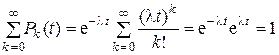При t = 1 получаем

.

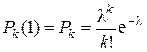Функция P_k(t) есть функция распределения дискретной случайной величины K. Из (2.7) следует, что она зависит от lt и k, а при t=1 –от l и k.

Как и для любой дискретной случайной величины, распределенной по закону Пуассона, математическое ожидание М(k) дисперсии D(k) и среднеквадратическое отклонение s(k) числа заявок простейшего потока, поступивших за отрезок времени t, равны: M(k) = D(k) = lt; s(k) = 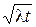. При t = 1 M(k) = D(k) = l, s(k) = .

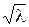Из этого следует, что интенсивность простейшего потока равна его параметру m = M(k) = l. Равенство m = l справедливо не только для простейшего потока, но и для любого стационарного ординарного потока.

Вероятность поступления k и более заявок определяется по формуле

.

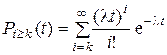Вероятности P_k(t) и P_i³k(t) для различных значений k и lt табулированы [11].

Функция F(z) распределения вероятностей промежутков времени между заявками.Согласно определению функция F(z) равна вероятности того, что промежуток времени между заявками будет меньше заданного промежутка z, что равносильно вероятности p₁(z) того, что за промежуток z поступит одна заявка и более. Используя (2.7), получим

F(z) = P(Z < z) = p₁(z) = p₀(z) – P₀(z) = 1 – e^–lZ, z ³ 0, (2.9)