Выбор безопасного пути судна с учетом точности его плавания
При плавании судна в море возникает необходимость рассчитать – на каком расстоянии следует пройти (обойти) навигационную опасность, чтобы безопасно «разойтись» с ней с заданной вероятностью (РЗАД).
Рассмотрим это на примере (рис. 18.15).
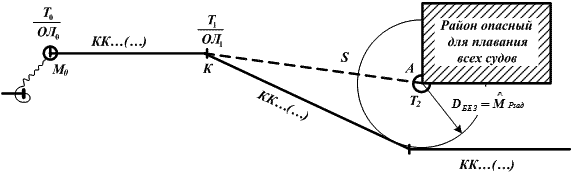
Рис. 18.15. Выбор безопасного пути судна с учетом точности его плавания
Задача: исключить вхождение в «Район опасный для плавания всех судов» с РЗАД.
Для решения этой задачи необходимо:
1. → исходную (упреждающую) точку, в которой будет изменен курс судна (т. К), соединить с навигационной опасностью (т. А);
2. → снять расстояние (S) между этими точками (т. К и т. А);
3. → рассчитать, сколько потребуется времени, чтобы судно прошло это расстояние с заданной скоростью → 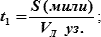
4. → рассчитать судовое время «прихода» в т. А → Т2 = Т1 + t1;
5. → рассчитать время плавания по счислению t = Т2 – Т0 (последний расчет СКП (М0) был в т. 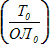 );
);
6. → по формуле (18.9) или (18.10) по КС и t рассчитать МСt;
7. → по формуле (18.22) рассчитать МСЧ;
8. → по формуле (18.23) по МСЧ и РЗАД рассчитать 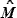 СЧ;
СЧ;
9. → от т. А (навигационной опасности) провести дугу окружности радиусом R = 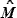 СЧРЗАД = DБЕЗ;
СЧРЗАД = DБЕЗ;
10. → из исходной точки (т. К) провести касательную к данной дуге и снять ее направление – искомая линия пути, следуя по которой судно пройдет навигационную опасность в DБЕЗ = 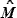 РЗАД.
РЗАД.
18.6.3. Задачи по расчету точности места судна (М0, МСt, МСЧ, 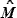 СЧ с РЗАД)
СЧ с РЗАД)
| № зад. | Условие | Ответ | ||||||||
| для расчета М0 по 2-м ЛП | КС | Время на которое рассчитывается МСЧ | М0 (мили) | МСt (мили) | МСЧ (мили) | 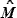 СЧ для Р = 95% (мили) СЧ для Р = 95% (мили)
| ||||
| Т0 (час) | mЛП1 (мили) | mЛП2 (мили) | θ° | |||||||
| 09.00 | ± 0,2 | ± 0,9 | 30° | 0,5 | 12.00 | 1,84 | 0,87 | 2,04 | 3,53 | |
| 10.00 | ± 0,3 | ± 0,8 | 35° | 0,6 | 12.00 | 1,49 | 0,84 | 1,71 | 2,96 | |
| 11.00 | ± 0,4 | ± 0,7 | 40° | 0,7 | 12.00 | 1,26 | 0,49 | 1,35 | 2,34 | |
| 12.00 | ± 0,5 | ± 0,6 | 45° | 0,8 | 16.00 | 1,10 | 1,60 | 1,94 | 3,36 | |
| 13.00 | ± 0,6 | ± 0,5 | 50° | 0,9 | 16.00 | 1,01 | 1,56 | 1,86 | 3,22 | |
| 14.00 | ± 0,7 | ± 0,4 | 55° | 1,1 | 16.00 | 0,98 | 1,54 | 1,83 | 3,17 | |
| 15.00 | ± 0,8 | ± 0,3 | 60° | 1,2 | 16.00 | 0,98 | 0,84 | 1,29 | 2,23 | |
| 16.00 | ± 0,9 | ± 0,2 | 65° | 1,3 | 20.00 | 1,01 | 2,60 | 2,79 | 4,83 | |
| 17.00 | ± 0,8 | ± 0,3 | 70° | 1,4 | 20.00 | 0,91 | 2,42 | 2,59 | 4,48 | |
| 18.00 | ± 0,7 | ± 0,4 | 75° | 1,5 | 20.00 | 0,83 | 2,10 | 2,26 | 3,91 |
Выводы
1. Любой измеренный навигационный параметр есть величина случайная и лишь с какой-то степенью достоверности соответствующая его истинному значению.
2. Все погрешности измерений делятся на 3 вида:
· случайные;
· систематические;
· грубые (промахи).
3. Случайные погрешности подчиняются закону нормального распределения (закону Гаусса).
4. Основной характеристикой оценки точности измерения навигационного параметра является СКП – средняя квадратическая погрешность.
5. Точность счислимого места принято оценивать радиальной или круговой СКП (МСЧ).
6. Вероятность нахождения счислимого места судна в круге, радиусом R = M составляет 0,63÷0,68 (63÷68%).
7. Коэффициент точности счисления (КС) характеризует скорость нарастания погрешности счисления по времени плавания по счислению.
8. Вероятнейшее значение навигационного параметра (UВ) соответствующего данной линии положения (навигационной изолинии), находится в полосе ±mЛП с вероятностью Р = 0,68 (68%).
9. Радиальная (круговая) СКП обсервованного места судна (М0) построена на полуосях эллипса погрешностей, а ее величина определяется по формуле:
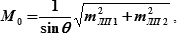 (мили)
(мили)
10. Погрешность счислимого (текущего) места судна складывается квадратически из погрешности исходной точки и погрешности счисления за время плавания от исходной точки до счислимого (текущего) места.
11. Учет погрешности счислимого (текущего) места судна – одна из важнейших гарантий его безопасного плавания.
Примечание: Самоконтроль знаний по теме проводится по тестовым заданиям к главе на базе приложения «Компьютерная система тестирования знаний «OPENTEST».
Дата добавления: 2021-01-26; просмотров: 751;











