Вещественный параметр. Непрерывный случай
Для большинства случайных процессов, которые рассматриваются в этом учебном пособии, множеством значений параметра служит некоторый интервал на вещественной оси R. В основном будут встречаться три случая: 1) T совпадает со всей прямой R = (–¥, +¥); 2) Т представляет собой положительную полуось [0, +¥); 3) Т является конечным интервалом [а, b]. Параметр t рассматривается как время.
Очень часто имеется прямое соответствие между результатами, полученными для процессов с непрерывным параметром, и аналогичными, обычно проще получаемыми, результатами для дискретного случая.
В § 1.4 мы видели, что в дискретном случае класс борелевских множеств в выборочном пространстве достаточно широк, чтобы включить все события, c которыми мы обычно встречаемся в приложениях. Даже если непосредственное вычисление вероятностей таких событий связано с большими трудностями, мы знаем, что они все равно однозначно определяются конечномерными распределениями. Если эти распределения известны, то вероятностная структура случайного процесса полностью определена.
Сделаем одно замечание для дискретного процесса. Пусть xn и hn – эквивалентные процессы (см. § 1.1), тогда xn и hn имеют одинаковые конечномерные распределения и Р(xn = hn) = 1 для каждого фиксированного n = 1, 2, … Так как n принимает лишь счетное множество значений, то отсюда следует , что Р(xn = hn для всех n = 1, 2, ...) = 1. Таким образом, можно сказать, что два эквивалентных дискретных процесса с вероятностью единица тождественны.
В непрерывном случае ситуация не столь проста. Выборочным пространством здесь является пространство Х всех конечных вещественных функций x(t) 0 £ t < ¥. Борелевские множества в Х были определены в § 1.3 как множества из наименьшего d-поля, cодержащего все интервалы. Каждое множество, полученное с помощью счетного числа операций над счетной совокупностью интервалов, является борелевским. На вероятностном языке это означает, что соответствующее событие определяется с помощью некоторых ограничений, наложенных на значения случайных величин x(t) в точках t1, t2, … из некоторого счетного множества. Вероятность любого такого события однозначно определяется конечномерными распределениями.
Однако очевидно, что многие события, вероятности которых мы хотели бы знать, нельзя определить таким образом. Каждому элементарному событию w соответствует определенная выборочная функция x(t) = x(t, w). Когда w пробегает пространство элементарных событий W, получаем совокупность «значений» соответствующей случайной функции x(t). Часто (в дальнейшем это будет видно) интересно знать вероятность того, что эта случайная функция обладает тем или иным свойством, которое определяется ее поведением в несчетном множестве точек t.
Например, может потребоваться знать вероятность того, что x(t) < h для всех t в некотором интервале I = [a, b], или вероятность того, что x(t) непрерывна, дифференцируема или интегрируема на I. События такого вида, вообще говоря, не являются борелевскими множествами и их вероятности не определяются однозначно конечномерными распределениями процесса. Иными словами, иногда можно найти два случайных процесса (при этом каждый из них задается некоторой функцией вида x(t, w)), имеющие одно и то же семейство конечномерных распределений, для которых вероятности таких неборелевских множеств не равны.
Покажем это на следующем примере.
Пример 1.2. Возьмем в качестве вероятностного пространства интервал Лебега [2] W = [0, 1] и равномерное распределение на нем. Определим случайные процессы x(t) и h(t) следующими соотношениями:
x(t) = x(t, w) = 0 для всех t и w,
h(t) = h(t, w) 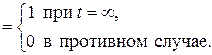
Очевидно, x(t) и h(t) имеют одно и то же семейство конечномерных распределений. Все эти распределения сосредоточены в начале координат, так что соответствующие функции распределения имеют вид
F(x1, …, xn; t1, …, tn) 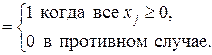
Тем не менее,
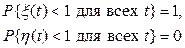 и
и 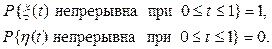
Таким образом, даже в примере сталкиваемся с событиями, вероят-ности которых не определяются однозначно конечномерными распределе-ниями.
Несколько изменив этот пример, можно показать, что даже вероят-ность того, что выборочная функция непрерывна в отдельной точке t = t0, не определятся однозначно конечномерными распределениями.
Пример 1.3. Действительно рассмотрим процесс x(t), определяемый соотношениями
n(t) = n(t, w) = 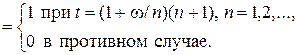
Конечномерные распределения остаются теми же, что и в примере 1.2, и x(0) = 0, n(0) = 0 для всех w, но
P{x(t) ® 0 при t ® 0} = 1,
P{n(t) ® 0 при t ® 0} = 0.
Все три процесса x(t), h(t), n(t) эквивалентны, т.к.
P{x(t) = h(t) = n(t) = 0} =1
для каждого фиксированного t. Однако
P{x(t) = h(t) = n(t) для всех t} = 0,
так что эти процессы не являются тождественными.
Как следует из приведенных примеров, вероятности многих событий, связанных со случайным процессом с непрерывным параметром, не определяются конечномерными распределениями этого процесса. Рассмотрим два возможных способа преодоления этого препятствия.
Первый способ.Пусть x(t) – случайный процесс с известными конечномерными распределениями. При каких условиях в терминах этих распределений существует процесс такой x0(t), что x(t) и x0(t) эквивалентны, т.е. P{x(t) = x0 (t)} = 1 для любого фиксированного t Î T, и выборочные функции процесса x0(t) с вероятностью единица обладают определенным свойством регулярности?
Если в рассматриваемом случае такой процесс x0(t) существует, то естественно изучать x0 вместо x, используя получаемое при этом упрощение.
Джордж Дуб [4] дал определениесвойства регулярности, которое он назвал сепарабельностью. По известному определению сепарабельная функция может быть в известном смысле восстановлена по ее значениям на некотором счетном всюду плотном множестве точек. Случайный процесс называется сепарабельным, если с вероятностью единица его выборочные функции обладают свойством регулярности. Дж. Дуб показал, что для любого случайного процесса x(t) можно найти эквивалентный ему сепарабельный процесс x0(t). Это решает сформулированную выше проблему в том случае, когда свойство регулярности совпадает с сепарабельностью.
Второй способ.Этот подход основан на использовании явного аналитического выражения, которым задается процесс x(t). Рассмотрим, например, функцию
x(t, w) = q(t, m1, m2, …),
где m1, m2, ... – конечное или счетное множество случайных величин (т.е. функций w); q – аналитическое выражение, содержащее t и mj. Если это выражение достаточно простое, то выборочные функции, полученные при фиксированных значениях mj, часто будут обладать свойством регулярности. Приведем пример использования этого метода.
Пример 1.4. Пусть r и q – независимые случайные величины, r > 0 и имеет плотность распределения 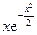 , а q равномерно распределена на [0, 2p]. Тогда функция x(t, w) = r cos (lt – q), где l – некоторое положительное число, определяет случайный процесс x(g) = x(t, w), который представляет собой гармоническое колебание с угловой частотой l, случайной амплитудой r и случайным сдвигом по фазе q. Все выборочные функции этого процесса непрерывны, так что вероятности событий, о которых говорилось раньше, однозначно определяются. Например, легко найти вероятность
, а q равномерно распределена на [0, 2p]. Тогда функция x(t, w) = r cos (lt – q), где l – некоторое положительное число, определяет случайный процесс x(g) = x(t, w), который представляет собой гармоническое колебание с угловой частотой l, случайной амплитудой r и случайным сдвигом по фазе q. Все выборочные функции этого процесса непрерывны, так что вероятности событий, о которых говорилось раньше, однозначно определяются. Например, легко найти вероятность
P{x(t) < h для всех t} = P{r < h} = 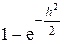 .
.
Дата добавления: 2021-01-11; просмотров: 634;











