Семейства случайных величин

ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

В практике научных исследований и технических разработок случайные процессы в настоящее время занимают столь большое место, что без создания эффективных методов их описания и изучения нельзя говорить о дальнейшем научно-техническом прогрессе.

Дать формальное определение случайного процесса, сочетающее в себе физическую сущность и математическую строгость, чрезвычайно трудно. Интуитивные представления о случайном процессе связаны в основном с непредсказуемостью его мгновенных значений. Математически строгое определение требует введения понятия ансамбля, т.е. бесконечной совокупности реализаций. С физической точки зрения вполне допустимо представление случайного процесса одной реализацией. С математической точки зрения отдельная реализация является детерминированной функцией времени, с помощью которой определить статистические свойства процесса можно лишь при выполнении определенных условий.

Выбор целесообразного уровня строгости описания случайных процессов при решении прикладных задач в значительной степени определяет качество получаемых результатов [1]. Вместе с тем уровень строгости описания должен соответствовать уровню представлений и характеру решаемых задач.

Семейства случайных величин

С точки зрения практических приложений [2] любая меняющаяся система, находящаяся под влиянием случайных факторов, представляет собой случайный процесс. В соответствии со сказанным случайный процесс может быть охарактеризован как процесс, мгновенное значение которого в произвольный момент времени представляет собой случайную величину [1].

Рассмотрим простой случай, когда состояние системы достаточно хорошо определяется одной количественной характеристикой. Эта величина x(t) в каждый фиксированный момент t не является однозначно определенной, как в случае детерминированных систем, а зависит от случайных факторов, которые влияли на систему до момента t. При построении математической модели этого процесса естественно рассматривать x(t) в каждый фиксированный момент t как случайную величину, определенную на некотором вероятностном пространстве (W, F, P). Когда t меняется в рассматриваемом промежутке времени, получаем семейство случайных величин x(t), зависящих от параметра t и определенных на одном и том же вероятностном пространстве. Элементарными событиями w в этом вероятностном пространстве будут возможные исходы случайного эксперимента, который определяет поведение системы в целом.

Пусть (W, F, Р) – некоторое вероятностное пространство, T – множество значений параметра. Случайным процессом называется конечная вещественная функция x(t, w),которая при каждом фиксированном t Î T является измеримой функцией от w Î W.

Легко получить обобщенную форму этого определения в случае, когда для полного описания состояния системы при каждом фиксированном значении параметра t необходимо знать несколько величин x₁(t), ..., x_n(t). Если рассматривать x_j(t) как компоненты случайного вектора x(t, w) = = {x₁(t, w), ..., x_n(t, w)}, то семейство случайных векторов, получающееся при изменении t на множестве Т, будет определять векторный случайный процесс.

Итак, x(t) – случайный процесс. При каждом фиксированном t = t₁ случайная величина x(t₁) = (t₁, w) имеет определенное распределение вероятностей, функцию распределения которой обозначим F(x, t₁) = P{x(t₁) £ £ x}.

Пусть t₁, ..., t_n – произвольное конечное множество значений t. Соответствующие случайные величины x(t₁), ..., x(t_n) имеют совместную функцию распределения

F(х₁, ..., х_n, t₁, ..., t_n) = Р{x(t₁) £ х₁, ..., x(t_n) £ x_n}.

Семейство таких совместных распределений для n = 1, 2, ... и всех возможных значений t_j называется семейством конечномерных распределений процесса x(t). Это одно из основных понятий теории, и многие существенные свойства случайного процесса определяются свойствами семейства его конечномерных распределений. Конечномерные распределения случайного процесса должны удовлетворять условиям симметрии и согласованности.

Условие симметрии требует, чтобы n-мерные функции распределения, введенные выше, были симметричными по всем параметрам (х_j, t_j), т.е. чтобы эти функции распределения не менялись при одновременной перестановке х_j и t_j.

Условие согласованности выражается соотношением

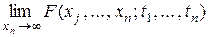= F(x_j, ..., x_n-1; t₁, ..., t_n-1),

которое следует из очевидного факта: w – множество, определенное неравенствами

x(t₁) £ x₁, ..., x(t_n-1) £ x_n-1, x(t_n) £ x_n,

при x_n ® ¥ приближается к множеству

{w, x(t1) £ x1, ..., x(tn-1) £ xn-1}.

Два случайных процесса x(t) и h(t) называются эквивалентными, если при каждом фиксированном t множества значений параметра x(t) и h(t) являются эквивалентными случайными величинами, так что x(t) = h(t) с вероятностью единица. Очевидно, семейства конечномерных распределений у эквивалентных процессов совпадают.

Выборочные функции

Случайный процесс может быть определен математически как функция двух переменных t и w, области изменения которых приведены в § 1.1. Причем, с одной стороны, x(t, w) при каждом фиксированном t является измеримой функцией элементарного события w, т.е. случайной величиной.

С другой стороны, x(t, w) для каждого фиксированного элементарного события w в данном вероятностном пространстве становится функцией от t, определенной для всех t Î Т. Иначе говоря, каждому w или каждому возможному исходу случайного эксперимента соответствует некоторая однозначно определенная функция от t. Эта функция x(t) = x(t, w) с фиксированным w описывает эволюцию (во времени, в пространстве или в каком-нибудь ином смысле) меняющейся системы в случае, когда элементарное событие w явилось результатом рассматриваемого случайного эксперимента. В соответствии с этим каждая функция x(t) называется реализацией, или траекторией, или выборочной функцией случайного процесса.

На рис. 1.1 показано по одной реализации четырех различных случайных процессов [3].

Рис. 1.1. Наблюдаемые значения случайных процессов: а – замирание интенсивности (l) радиосигналов; б – пульсация температуры (Т) воздуха в точке атмосферы; в – пульсация разности скоростей (DV) ветра в двух точках атмосферы, находящихся на расстоянии 8 см друг от друга; г – изменение диаметра (Dd) ткацкой нити вдоль длины нити

Реализация x(t) может рассматриваться как «точка» в пространстве x всех конечных вещественных функций x(t) переменного t Î T. Пространство x называется пространством выборочных функций или просто выборочным пространством случайного процесса.

Случайный процесс x(t, w) определяет функцию, переводящую каждую точку w вероятностного пространства (W, F, Р) в некоторую точку пространства выборочных функций x. Эта функция индуцирует некоторое распределение вероятности в x. Множество А¹ из x является множеством функций от t. Отсюда, каждое множество функций А¹ имеет прообразом некоторое w-множество А, состоящее из всех точек w, таких, что соответствующие функции x(t) = x(t, w) принадлежат А¹. Индуцированная вероятностная мера Р¹ в x определяется для всех А¹ Î F соотношением Р¹(А¹) = Р(А). Тройка (x, F¹, Р¹) представляет собой новое вероятностное пространство, соответствующее индуцированному распределению.

На вероятностном языке Р¹(А¹) означает вероятность того, что реализация x(t) случайного процесса будет принадлежать множеству А¹ пространства всех выборочных функций x. Поэтому x(t) можно рассматривать как случайную функцию, принимающую различные «значения» в x в соответствии с вероятностной мерой Р¹(А¹).

При изучении важных классов случайных процессов, как и в различных приложениях, нас будут интересовать свойства распределений вероятности в выборочном пространстве, индуцированных рассматриваемыми процессами. Например, потребуется находить вероятность того, что реализации данного процесса обладают тем или иным свойством, т.е. принадлежат некоторому определенному множеству А¹ функционального пространства Х.

В связи с этим возникает вопрос: в какой степени распределение вероятностей в выборочном пространстве x, индуцированное данным процессом, определяется семейством конечномерных распределений этого процесса? Кроме того, если на множестве значений параметра T задано некоторое семейство конечномерных распределений, то при каких условиях существует случайный процесс, имеющий эти распределения?

Ответ на эти вопросы содержится в теореме Колмогорова, которая будет представлена в следующем разделе.