Общие свойства случайных процессов

Рассмотрим событие Е, происходящее в случайные моменты времени. Пусть N(s, t) обозначает их число в полуинтервале (s, t]. Вероятностную структуру N(s, t) определяют, как и в пуассоновском случае, возрастающие ступенчатые функции x(t), которые будут задаваться на всей прямой – ¥ < t < + ¥. Как и в пуассоновском случае, N(s, t) будет определяться соотношением N(s, t) = x(t) – x(s). Предположим, что для любого конечного числа непересекающихся интервалов (s₁, t₁], …, (s_k, t_k] заданы вероятности

P{N(s₁, t₁) = r₁, …, N(s_k, t_k) = r_k},

согласованные в том смысле, что

,

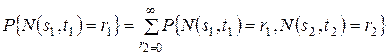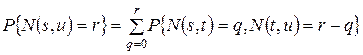, s < t < q, и т.п.

Так как рассматриваются полузамкнутые интервалы (s, t], то необходимо, чтобы функции вида Р{N(s, t) = r} были непрерывны справа по t. Эти вероятности определяют конечномерные распределения процесса x(t) и, следовательно, вероятностную меру на функциональном пространстве Х. Так же как для пуассоновского процесса, построим эквивалентный вариант x(t), реализации которого не убывают и в любом конечном интервале имеют не более конечного числа скачков. Эти скачки будут соответствовать появлениям событий рассматриваемого потока (читатель может провести это построение самостоятельно). В дальнейшем не будем обращать внимание на основной процесс x(t), а будем рассматривать лишь случайные величины N(s, t).

Согласно работе [5] случайный процесс является стационарным, если для любого конечного числа интервалов (s₁, t₁], …, (s_k, t_k], любых чисел (целых) r₁, …, r_k и любого r > 0

Р{N(s_i + t, t_i + t) = r_i, i = 1, …, k} = P{N(s_i, t_i) = r_i, i =1, …, k}.

Это и есть общие условия 1, сформулированные ранее для пуассоновского случая.

Стандартный процесс будет называться ординарным [2], если

Р{N(0, t) >1} = 0(t) при t ® 0.

Это уточнение условия 3 для пуассоновского процесса.

Рассмотрим следующую лемму, которая очень полезна при изучении свойств процессов.

Лемма 1. Пусть f (x) – вещественная неотрицательная и неубывающая функция в интервале 0 < x £ a и ¦(x + y) £ ¦(x) + ¦(y), когда х, y, x + y Î Î (0, a). Тогда при х ® 0 отношение ¦(x)/x стремится к некоторому пределу, быть может бесконечному. Этот предел равен нулю лишь при условии ¦(a) = 0.

Положим w(t) = Р{N(0, t) ³ 1}. С помощью леммы можно доказать [5] существование такого неотрицательного l £ ¥, что

w (t) ~ lt при t ® 0. (1.4)

Действительно, w(t), очевидно, не убывает по t. Далее, если в интервале (0, t₁ + t₂) произошло хотя бы одно событие, то, по крайней мере, в одном из интервалов (0, t₁] и (t₁, t₁ + t₂] тоже произошло хотя бы одно событие и, следовательно, w(t₁ + t₂) £ w(t₁) + w(t₂), так что условия леммы выполнены. Таким образом, w(t)/t стремится к некоторому пределу при t, откуда следует (1.4). Число l в (1.4) называется интенсивностью стационарного процесса. Очевидно, l всегда строго положительно, за исключением тривиального случая, когда ни одно из событий не происходит.

Приведенные выше рассуждения касаются стационарного процесса без требования ординарности. Если же стационарный процесс ординарен, то вероятность того, что два или более события произойдут одновременно хотя бы в одной точке, равна нулю. Действительно, разделим отрезок [0, 1] на m равных частей, тогда интересующая нас вероятность не превосходит mP{N(0, m^-1) >1}, которая стремится к нулю при m ® ¥. Обратное утверждение содержится в следующей лемме [2].

Лемма 2. Рассмотрим стационарный поток событий, для которого вероятность того, что хотя бы в одной точке отрезка 0 £ t £ 1 произойдут одновременно два или более события, равна нулю. Пусть m = e{N(0,1)} < ¥. Тогда процесс ординарен.

Лемма доказана Добрушиным при условии m = e{N(0, 1)} < ¥. Разумеется, это не исключает возможности существования ординарного потока c m = +¥.

Из эвристических соображений ясно, что для стационарного регулярного (ординарного) процесса среднее число событий в единичном интервале m и интенсивность процесса, определенная (1.4), совпадают. Доказательство этого, данное Хинчиным [5], опирается на следующую теорему.

Теорема. Рассмотрим стационарный регулярный процесс. Утверждается, что среднее число событий в единицу времени m и интенсивность потока l, определенная соотношением (1.4), совпадают. Случай l = m = +¥ при этом не исключается.

Итак, мы рассмотрели основные общие свойства случайных процессов, которые нам понадобятся в последующих главах.