Метод проверки гипотез о законах распределения.
Задача проверки гипотезы о законах распределения начинается с выбора нулевой гипотезы. Предлагается следующая методика. По данным эксперимента определяются статистические оценки коэффициента ассиметрии 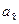 и коэффициента эксцесса
и коэффициента эксцесса 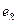 [1-5,13,14].
[1-5,13,14].
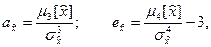
где
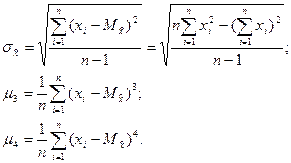
В теории распределений доказано, что каждому закону свойственно определенное соотношение между коэффициентами ассиметрии и эксцесса, то есть может быть простроена диаграмма, построенная на рис.12.4.
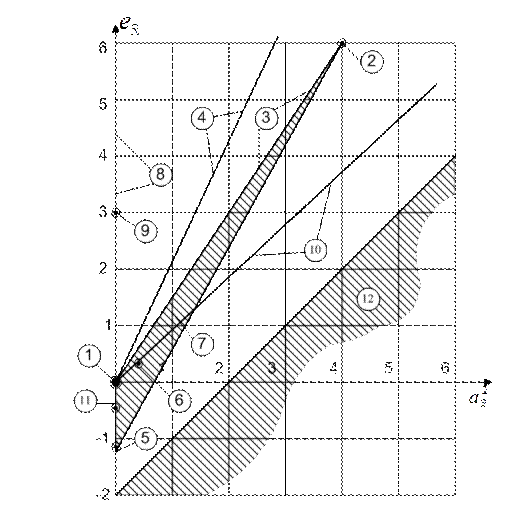
Рис.12.6. Диограмма для выбора вида закона распределения
На рис.12.4. выделены следующие характерные области и точки. Точки (0; -1,2); (0;0); (0;3); (4;6) отвечают соответственно равномерному и нормальным распределениям, распределению Лапласа и показательному распределению. Так, для любого нормального распределения 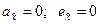 , что определяет координаты точки II. Гамма-распределение, логнормальное, распределения Стьюдента и Пуассона показаны на диаграмме прямыми, а бета-распределение представлено областью. На рисунке обозначено: I – равномерный закон; II – нормальный закон; III – закон Лапласа; IV – бета-распределение; V – закон Стьюдента; VI – гамма-распределение; VII – закон Пуассона; VIII – показательный закон; IX – логнормальное распределение.
, что определяет координаты точки II. Гамма-распределение, логнормальное, распределения Стьюдента и Пуассона показаны на диаграмме прямыми, а бета-распределение представлено областью. На рисунке обозначено: I – равномерный закон; II – нормальный закон; III – закон Лапласа; IV – бета-распределение; V – закон Стьюдента; VI – гамма-распределение; VII – закон Пуассона; VIII – показательный закон; IX – логнормальное распределение.
При попадании точки в области диаграммы, для которых не определен закон распределения, выдвижение гипотетического закона должно осуществляться на основании каких-либо дополнительных априорных соображений.
Знание оценок 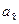 и
и 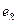 позволяет приближенно определить закон распределения. Для этого по полученным значениям оценок на диаграмму наносится точка
позволяет приближенно определить закон распределения. Для этого по полученным значениям оценок на диаграмму наносится точка 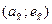 . Если она окажется вблизи от точки, прямой или области, соответствующей одному из распределений, то последнее и следует выдвинуть в качестве гипотезы.
. Если она окажется вблизи от точки, прямой или области, соответствующей одному из распределений, то последнее и следует выдвинуть в качестве гипотезы.
Задача проверки гипотезы о виде распределения происходит по методу Колмогорова. В качестве показателя согласованности используется величина:
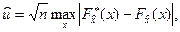
где 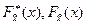 - соответственно статистическая и теоретическая (гипотетическая) функции распределения СВ
- соответственно статистическая и теоретическая (гипотетическая) функции распределения СВ 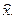
Дата добавления: 2016-09-26; просмотров: 2079;











