Графические методы.

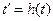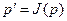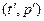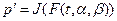Эти методы применимы для некоторых семейств функций распределения F(t, α, β), содержащих два неизвестных параметра α, β. График функции F(t, α, β) можно представить в виде совокупности точек на плоскости (t, p), где p=F(t,α,β). Основная идея графического метода состоит в том, что подбирается такая непрерывная замена координат , , что при этом график функции распределения на плоскости , где , становится прямой линией 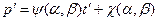(12.8). Используем этот факт для оценки параметров α, β.

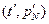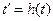Предположим, что в результате испытаний получены N значений некоторой случайной величины (например, времени безотказной работы). По этим значениям мы можем построить эмпирическую функцию распределения F(t, α, β), то после замены переменных график , где , а 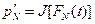, будет лежать в непосредственной близости от графика 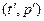, являющегося прямой вида (12.8). Оценив с помощью линейки тангенс угла наклона “k” и свободный член “b” и приравняв их теоретическим значениям, получаем уравнения: k= Ψ(α, β), b=χ(α, β) (12.9), из которых находим оценки неизвестных значений параметров α и β. Заметим, что графический метод применим для любого из планов [N, U, r], [N, R, r], [N, U, T], [N, R, T], [N, U, (r, T)], [N, R, (r, T)]. Например, в случае плана [N, U, (r, T)] по результатам испытаний можем построить только часть 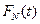для значений t≤min(t_r,T) и 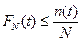, где n(T)≤r – число изделий, отказавших во время проведения испытаний. Если к полученному куску эмпирической функции распределения применить преобразования 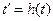, , 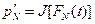то на плоскости 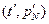получим кусок ломаной, близкой одной из прямых вида (1.2.8). По этому куску оцениваем “k” и “b” и снова приходим к уравнениям (1.2.9).

Рассмотрим пример.

Пусть имеем нормальное распределени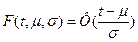е: , где 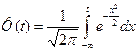обозначим 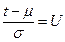. Тогда 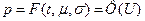. Таким образом “U” – квантиль уровня “P” нормального распределения. В качестве преобразования J(P) рассмотрим функцию 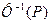, обратную к функции P=Ф(t). При этом получаем

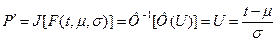. (12.10).

Таким образом, (12.10) соответствует (12.9), когда 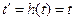; ; 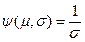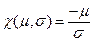. Для удобства использования выпускается специальная координатная шкала, по оси абсцисс отложены значения t случайной величины, a по оси ординат значения функции 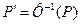. Около каждого значения 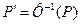отмечается соответствующее ему значение P. Так как 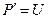, то 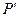является квантилью уровня “P” нормального распределения.

Если задан вариационный ряд: t₁ ≤ t₂ ≤ …≤ t_N, то зная 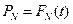по таблице квантилей находим 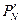- квантиль уровня “ 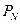” нормального распределения. Значение P_N=0.99 соответствует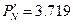

По значениям 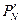и t строим ломаную линию.

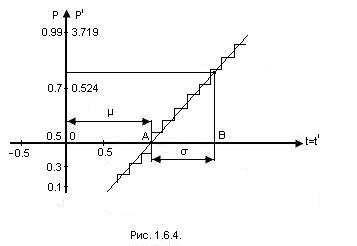
Рис. 12.7.

С помощью вероятностной бумаги можно легко проверять нормальность закона распределения, а заодно и оценивать его параметры. Если ломаная имеет заметную искривлённость, то это говорит о том, что истинный закон распределения не является нормальным. Если же искривлённости нет, то проводя “на глаз” прямую, наиболее плотно прилегающую к ломанной, легко находим оценки для μ и σ: μ равно абсциссе точки А, где А – точка пересечения прямой с осью “t”; σ равно расстоянию AB, где “B” точка на оси t, в которой величина перпендикуляра, опущенного из точки прямой на ось t, равна 1 (рис. 12.4.) (в единицах масштаба оси абсцисс).