Оптимальное резервирование
Задача оптимального резервирования заключается в выборе числа и распределения резервных элементов, обеспечивающих в определённом смысле оптимальность всего резервного соединения. Задача на оптимальное резервирование возникает тогда, когда существует определённое ограничение на затрачиваемые для повышения надёжности средства [20,21].
Постановка задачи:
Пусть имеется некоторая реальная система, состоящая из неопределённого числа различных элементов, составленных на логической схеме последовательное соединение (рис 11.4-а):
|
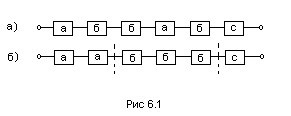
Перестраиваем эту систему, объединяя однотипные элементы в условные подсистемы (рис. 11.4 -б). Обозначим: xi (i=1..n) – количество резервных элементов;
X(x1, x2..xn) – вектор состава резервных элементов;
Pi(xi) – функция надёжности для i-ой подсистемы, содержащей xi резервных элементов.
P(X) – функция надёжности системы с вектором X состава резервных элементов.
С(X) – затраты на резервирование системы при одном лимитирующем факторе.
Cj(X) (j=1..m) – затраты на резервирование при наличие j лимитирующих факторов.
Можно записать: 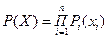 , причём
, причём 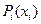 может быть определена для каждого конкретного способа резервирования.
может быть определена для каждого конкретного способа резервирования.
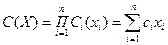 , где ci - “стоимость” одного элемента i-го типа.
, где ci - “стоимость” одного элемента i-го типа.
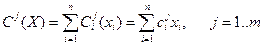
Возможна постановка следующих двух задач оптимального резервирования:
1. Прямая задача:
Найти число резервных элементов xi(i=1..n) для каждой i-ой подсистемы, обеспечивающих заданное значение показателя надёжности системы при минимальных затратах, т.е.
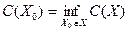 при
при 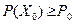 (11.16)
(11.16)
где P0 – заданное значение функции надёжности системы;
X0 – вектор состава резервных элементов оптимальной системы.
2. Обратная задача.
Найти число резервных элементов xi(i=1..n) подсистемы, обеспечивающих максимальный показатель надёжности Р(Х) при величине затрат не превышающих заданную, т.е.
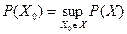 при
при 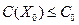 (11.17)
(11.17)
где С0 – заданная “стоимость” системы. Для нескольких ограничивающих факторов - 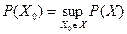 при
при 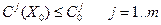
Дата добавления: 2016-09-26; просмотров: 4513;











