Логико-вероятностный метод

В ряде случаев объект или систему невозможно представить со­стоящей из параллельно-последовательных соединений. Особенно это от­носится к цифровым электронным информационным системам, в которых для повышения надежности вводятся перекрестные информационные свя­зи. На рис. 9.17 изображена часть структуры системы с перекрестными свя­зями (стрелки показывают возможные направления перемещения информации в системе). Для оценки надежности таких структур действенным оказывается логико-вероятностный метод.

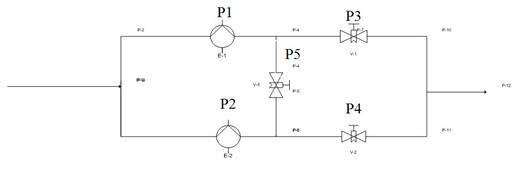
Рис. 9.17 Мостиковая схема подачи топлива;

1-2 –насосы, 3,4,5 – клапаны

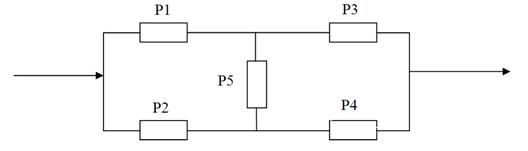
Рис. 9.18 Мостиковая схема измерительно-вычислительного комплекса;

1,2 – запоминающее устройство; 3,4 – процессоры; 5 – блок, обеспечивающий двустороннюю передачу цифровых данных.

В методе работоспособное состояние структуры предлагается описы­вать с помощью аппарата математической логики с последующим фор­мальным переходом к вероятности безотказной работы оцениваемой сис­темы или устройства. При этом через логическую переменную x_j обозначается событие, заключающееся в том, что данный i-й элемент работоспособен. Формально работоспособное состояние всей системы или объекта отображается логической функцией, называемой функцией работоспособности. Для нахождения этой функции необходимо определить, следуя от входа к выходу структуры системы все пути движения информации и рабочего тела, отвечающему работоспособному состоянию системы. Например, на рис. 9.17. таких путей четыре: путь 1 – 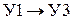, путь 2 - 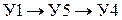, путь 3 – 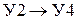, путь 4 – .

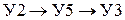Зная все пути, отвечающие работоспособному состоянию структуры можно записать в символах алгебры логики в дизъюнктивно – конъюктивной форме функцию работоспосбности (X)/ Например для рис. 9.17 это:

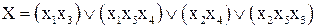(9.35)

Применяя известные методы минимизации, логическую функцию работоспособности, упрощают и переходят от нее к уравнению работоспособности системы в символах обычной алгебры. Осуществляется такой переход формально с использованием известных соотношений (слева логическая запись, справа алгебраическая):

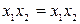, (9.36)

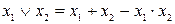, (9.37)

. (9.38)

Вероятность безотказной работы объекта (см. рис. 9.16, 9.17) в целом определяется формальной подстановкой в алгебраическое выражение функции работоспособности вместо переменных 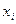значение вероятностей безотказной работы каждого i-ого элемента системы.

Пример. Необходимо найти в общем виде вероятность безотказной работы объектов, структура которых представлена на рис. 9.16 и 9.17. Несмотря на различные элементные базы элементы структуры этих объектов с точки зрения формальной логики идентичны. В связи с этим для наглядности на рис. 9.17 элементы У1, У2 – два одинаковых равнонадежных насоса с вероятностями безотказной работы 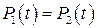. Элементы У3, У4 – два равнонадежных процессора с вероятностью безотказной работы 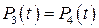. Элемент У5 – переключающий клапан, обеспечивающий двустороннюю подачу рабочего тела (например топлива) на выходе объекта.

Аналогичным образом выглядит структура объекта на рис. 9.17, где элементы У1, У2 два одинаковых равнонадежных запоминающих устройства (ЗУ), с вероятностью безотказной работы 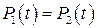. Элементы У3, У4 – два одинаковых равнонадежных процессора с вероятностью безотказной работы 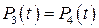. Элемент У5 блок, обеспечивающий двустороннюю передачу цифровых данных. Вероятностью безотказной работы этого блока .

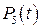Учитывая (9.36), (9.37), (9.38) можно произвести формальный переход от записи (9.35) к алгебраической форме записи. Так для нахождения логической функции работоспособности объекта возможные пути прохождения информации (рабочего тела) от входа к выходу имеют вид:

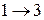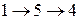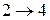или или или ,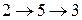

Откуда с учетом (9.35) осуществляется формальный переход от записи (9.35) к алгебраической форме записи:

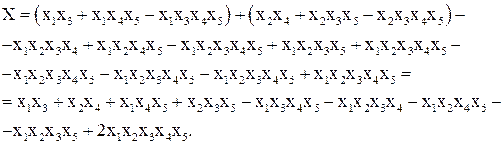
(9.39)

От (9.39) переходим к вероятности безотказной работы всего устройства путем формальной замены 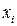на 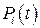. При этом, опуская аргумент 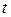и принимая во внимание, что и 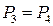, получим окончательно

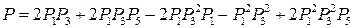; (9.40)

При всех равнонадежных элементах 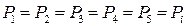выражение (9.40) примет вид:

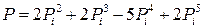. (9.41)