Показатели безотказности объектов с мгновенным восстановлением.
Допущение о мгновенном восстановлении работоспособности может быть принято только в том случае, когда время восстановления существенно меньше времени наработки на отказ.
Сущность модели восстанавливаемого объекта с мгновенным восстановлением заключается в следующем (рис. 3.5): в момент начала работы t = 0 объект работоспособен; проработав случайное время 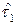 , объект переходит в неработоспособное состояние, т.е. в случайный момент времени
, объект переходит в неработоспособное состояние, т.е. в случайный момент времени 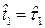 возникает первый отказ; затем следует мгновенное и полное восстановление работоспособности объекта; проработав случайное время
возникает первый отказ; затем следует мгновенное и полное восстановление работоспособности объекта; проработав случайное время 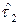 , объект снова переходит в неработоспособное состояние, т.е. в случайный момент времени
, объект снова переходит в неработоспособное состояние, т.е. в случайный момент времени 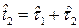 возникает второй отказ; снова следует мгновенное и полное восстановление работоспособности объекта и т.д.
возникает второй отказ; снова следует мгновенное и полное восстановление работоспособности объекта и т.д.
|
|
|
|
|
|
|
|
|
|
|
| |
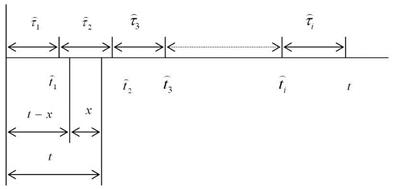
Рис. 3.5. Модель восстанавливаемого объекта с мгновенным восстановлением
Интервалы времени между отказами 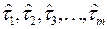 являются конкретными реализациями случайного времени
являются конкретными реализациями случайного времени 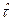 между отказами. Случайная величина времени
между отказами. Случайная величина времени 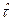 между отказами, которая характеризуется функцией распределения и плотностью распределения, выражения для которых соответственно имеют вид:
между отказами, которая характеризуется функцией распределения и плотностью распределения, выражения для которых соответственно имеют вид:
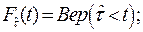 (3.22)
(3.22)
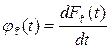 . (3.23)
. (3.23)
Моменты времени возникновения 1, 2,…, i-го, …, m-го отказов:
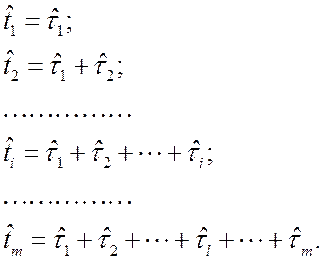
образуют поток отказов, а так как восстановление происходит мгновенно, то эти же моменты образуют и поток восстановлений. Моменты времени 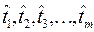 являются случайными величинами и характеризуются функциями распределения
являются случайными величинами и характеризуются функциями распределения 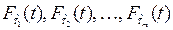
Функции распределения 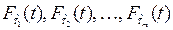 - это вероятности того, что первый, второй,…,
- это вероятности того, что первый, второй,…, 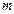 -ый отказы произойдут за время
-ый отказы произойдут за время 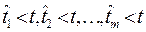 , где
, где 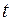 - заданное время (наработка).
- заданное время (наработка).
Процесс отказов (восстановлений) можно описать случайной величиной 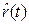 , равной числу отказов (восстановлений) за время (наработку)
, равной числу отказов (восстановлений) за время (наработку) 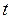 . Естественно, что
. Естественно, что 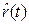 принимает только целые неотрицательные значения.
принимает только целые неотрицательные значения.
Функция распределения дискретной случайной величины 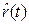 [2-5]
[2-5]
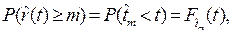 (3.24, а)
(3.24, а)
где 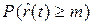 - вероятность того, что в момент времени
- вероятность того, что в момент времени 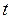 число отказов
число отказов 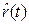 будет больше или равно числу m;
будет больше или равно числу m;
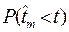 - вероятность того, что m-ый отказ произойдет в момент времени
- вероятность того, что m-ый отказ произойдет в момент времени 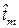 , который меньше t.
, который меньше t.
Так как события 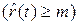 и
и 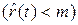 образуют полную группу несовместимых событий, то
образуют полную группу несовместимых событий, то 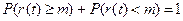 , и вероятность возникновения числа отказов меньше m.
, и вероятность возникновения числа отказов меньше m.
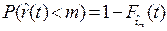 . (3.24, б).
. (3.24, б).
Исходя из свойств функции распределения (3.24, а), вероятность возникновения ровно 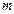 отказов в течение времени
отказов в течение времени 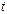 с учетом (3.24, б)
с учетом (3.24, б)
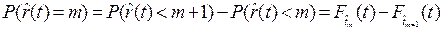 . (3.24,в)
. (3.24,в)
В теории надежности принято случайную величину числа отказов 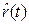 характеризовать функцией восстановления
характеризовать функцией восстановления 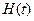 или ведущей функцией потока, под которой понимается математической ожидание числа отказов (восстановлений) за время (наработку) t [2-5,15]
или ведущей функцией потока, под которой понимается математической ожидание числа отказов (восстановлений) за время (наработку) t [2-5,15]
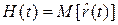 , (3.25)
, (3.25)
где 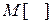 - символ математического ожидания.
- символ математического ожидания.
Известно, что математическое ожидание дискретной случайной величины есть сумма произведений возможных значений случайной величины на вероятности их возникновения. Следовательно, функция восстановления может быть определена по формуле математического ожидания [2,5,15]
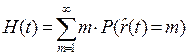 , (3.26)
, (3.26)
где m - конкретные значения случайной величины числа отказов 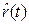 ;
;
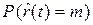 - вероятности возникновения ровно m отказов, m=1,2,3,… .
- вероятности возникновения ровно m отказов, m=1,2,3,… .
Формула (3.26) с учетом (3.24, в) преобразуется к виду
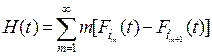 .
.
Если раскрыть сумму в правой части последнего равенства и произвести приведение подобных членов, то будет иметь место следующее выражение
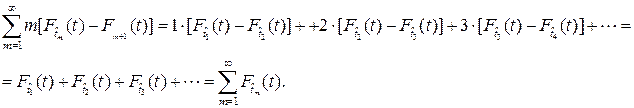
Следовательно, выражение для функции восстановления преобразуется к виду
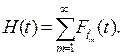 (3.27)
(3.27)
Зная распределение случайной величины 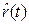 , можно, например, рассчитать на данный (планируемый) период вероятной число отказов, а, следовательно, и число необходимых запасных элементов в составе ЗИП.
, можно, например, рассчитать на данный (планируемый) период вероятной число отказов, а, следовательно, и число необходимых запасных элементов в составе ЗИП.
Несмотря на то, что функция восстановления 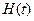 полностью характеризует поток отказов (восстановлений), ее использование ограничено только нормальным экспоненциальным распределением и гамма-распределением. Поэтому для описания безотказности восстанавливаемых объектов используются параметр потока отказов
полностью характеризует поток отказов (восстановлений), ее использование ограничено только нормальным экспоненциальным распределением и гамма-распределением. Поэтому для описания безотказности восстанавливаемых объектов используются параметр потока отказов 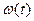 и средняя наработка на отказ
и средняя наработка на отказ 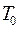 .
.
Параметр потока отказов, или плотность отказов 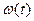 - отношение среднего числа отказов восстанавливаемого объекта за бесконечно малую наработку к значению этой наработки, т.е.
- отношение среднего числа отказов восстанавливаемого объекта за бесконечно малую наработку к значению этой наработки, т.е.
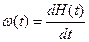 . (3.28)
. (3.28)
После дифференцирования (3.27) для параметра потока отказов 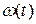 имеет место
имеет место
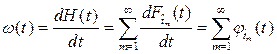 , (3.29)
, (3.29)
где 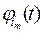 - плотность распределения случайной величины
- плотность распределения случайной величины 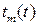 .
.
Несмотря на некоторую cхожесть параметра потока отказов 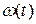 и интенсивности отказа
и интенсивности отказа 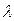 , они как по определению, так и по существу различные, а именно:
, они как по определению, так и по существу различные, а именно:
интенсивность отказов – условная плотность вероятности возникновения отказа, определяемая при условии, что до рассматриваемого момента времени отказ не наступил;
параметр потока отказов – безусловная вероятность возникновения отказа за единицу времени.
Только для периода нормальной эксплуатации численные значения параметра отказов и интенсивности отказов равны, т.е. 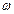 =
= 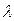 .
.
Средняя наработка на отказ 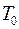 - отношение суммарной наработки
- отношение суммарной наработки 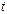 восстанавливаемого объекта к математическому ожиданию числа его отказов
восстанавливаемого объекта к математическому ожиданию числа его отказов 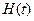 в течение этой наработки.
в течение этой наработки.
Согласно этому определению средняя наработка на отказ
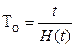 . (3.30)
. (3.30)
С целью существенного упрощения изложения в дальнейшем рассматриваются потоки событий, удовлетворяющие свойствам: ординарности, отсутствия последействия и стационарности.
Поток событий называют ординарным, если вероятность попадания на интервал времени 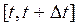 двух и более событий пренебрежимо мало (стремится к нулю) при стремлении длины интервала
двух и более событий пренебрежимо мало (стремится к нулю) при стремлении длины интервала 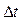 к нулю. Как показывает опыт эксплуатации технических устройств, одновременное возникновение двух и более отказов маловероятно.
к нулю. Как показывает опыт эксплуатации технических устройств, одновременное возникновение двух и более отказов маловероятно.
Поток событий называется потоком без последействия, если вероятность попадания m событий на интервал времени 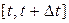 не зависит от числа и моментов появления событий на других интервалах, не пересекающихся с данным.
не зависит от числа и моментов появления событий на других интервалах, не пересекающихся с данным.
Если поток событий является ординарным и без последействия, то число событий, попадающих на интервал времени 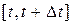 , распределено по закону редких явлений или закону Пуассона. Такой поток называют пуассоновским [2-5,18]. Для пуассоновского потока вероятность того, что случайная величина числа событий
, распределено по закону редких явлений или закону Пуассона. Такой поток называют пуассоновским [2-5,18]. Для пуассоновского потока вероятность того, что случайная величина числа событий 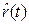 , попавших на интервал
, попавших на интервал 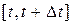 , выражается формулой Пуассона
, выражается формулой Пуассона
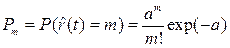 , (3.31)
, (3.31)
где a - параметр закона Пуассона (математическое ожидание числа событий, попадающих на интервал 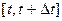 );
);
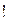 - символ факториала.
- символ факториала.
Параметр закона Пуассона определяется формулой [5,15,18]
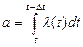 ,
,
где 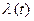 - интенсивность потока.
- интенсивность потока.
Принято считать, что пуассоновский поток отказов характерен для сложных нерезвированных объектов, состоящих из высоконадежных элементов, потоки отказов которых являются независимыми.
Для таких потоков вероятность безотказной работы на интервале [t1,t2] будет определяться формулой
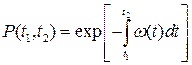 . (3.32)
. (3.32)
Если вероятность попадания m событий на интервал времени 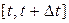 зависит только от числа m событий и длины интервала
зависит только от числа m событий и длины интервала 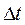 и не
и не
зависит от начала интервала t, то такой поток называют стационарным.
Пуассоновский поток, удовлетворяющий условиям стационарности, называется простейшим [2-5,18].
Для простейшего потока число событий, попадающих в произвольный интервал длиной 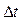 , распределено по закону Пуассона (3.31) с параметром
, распределено по закону Пуассона (3.31) с параметром 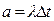
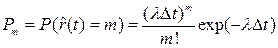 . (3.33)
. (3.33)
В свою очередь, распределение времени между событиями в простейшем потоке подчинено экспоненциальному закону с плотностью распределения
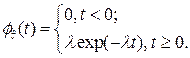 (3.34)
(3.34)
Для простейшего потока отказов, когда 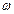 =
= 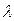 , справедливы следующие формулы [2-5]:
, справедливы следующие формулы [2-5]:
вероятность возникновения ровно 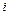 отказов
отказов
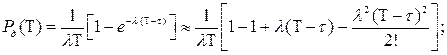 (3.35)
(3.35)
вероятность возникновения не более 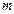 отказов
отказов
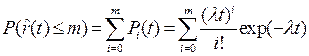 ; (3.36)
; (3.36)
функция восстановления
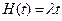 ; (3.37)
; (3.37)
наработка на отказ
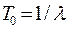 ; (3.38)
; (3.38)
вероятность безотказной работы, когда число отказов 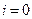 ,
,
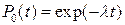 . (3.39)
. (3.39)
Оценка параметра потока отказов по статистической информации проводится для каждого интервала наработки 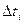 по формуле
по формуле
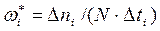 , (3.40, а)
, (3.40, а)
где 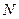 - число восстанавливаемых объектов, находящихся в эксплуатации;
- число восстанавливаемых объектов, находящихся в эксплуатации;
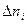 - число отказов всех объектов на интервале
- число отказов всех объектов на интервале 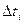 .
.
Если оценка параметра потока отказов проводится по одному объекту, т.е. 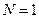 , то она характеризует число отказов объекта в единицу времени и определяется по формуле
, то она характеризует число отказов объекта в единицу времени и определяется по формуле
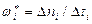 . (3.40, б)
. (3.40, б)
Оценка наработки на отказ определяется как отношение суммарной наработки 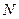 восстанавливаемых объектов к суммарному числу отказов этих объектов:
восстанавливаемых объектов к суммарному числу отказов этих объектов:
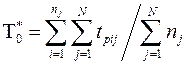 , (3.41, а)
, (3.41, а)
где 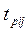 -
- 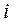 -я наработка
-я наработка 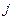 -го объекта;
-го объекта;
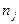 - число отказов
- число отказов 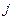 -го объекта.
-го объекта.
Для одного объекта оценка наработки на отказ проводится по формуле
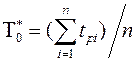 , (3.41, б)
, (3.41, б)
где 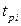 - наработка на i-й отказ;
- наработка на i-й отказ;
n - число отказов.
Пример 3.3. Для восстанавливаемого объекта, отказы-восстановления которого образуют простейший поток с параметром потока 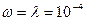 1/ч, рассчитать вероятности возникновения одного, двух, …, пяти отказов и другие рассмотренные показатели безотказности для наработки
1/ч, рассчитать вероятности возникновения одного, двух, …, пяти отказов и другие рассмотренные показатели безотказности для наработки 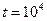 ч.
ч.
Решение:
1. Наработка на отказ 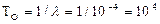 ч.
ч.
2. Функция восстановления 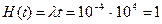 отказ.
отказ.
3. Вероятность безотказной работы
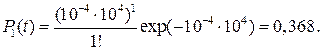
4. Вероятности возникновения одного, двух, ..., пяти отказов рассчитанных по формуле (3.35) равны соответственно:
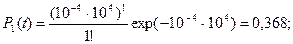
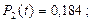
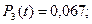
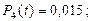
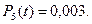
5. Вероятность возникновения не более пяти отказов рассчитана по формуле (3.36) и равна
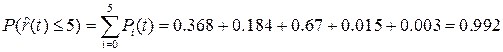 .
.
Параметры потока отказов мгновенно восстанавливаемых объектов определяются следующим образом.
В общем случае среднее количество отказов (замен) 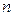 на интервале
на интервале 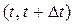 пропорционально числу
пропорционально числу 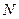 находящихся под наблюдением объектов и продолжительности интервала наработки
находящихся под наблюдением объектов и продолжительности интервала наработки 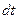 :
:
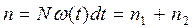 ,
,
где 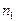 - количество отказов объектов из числа безотказно проработавших в течение интервала
- количество отказов объектов из числа безотказно проработавших в течение интервала 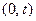 ;
; 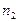 - количество отказов объектов из числа уже отказавших ранее.
- количество отказов объектов из числа уже отказавших ранее.
Очевидно, что
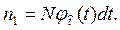
Для определения среднего количества отказов объектов из числа уже отказавших ранее рассматривается малый интервал наработки 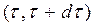 , предшествующий t. В течение этого интервала отказало и заменено на новые
, предшествующий t. В течение этого интервала отказало и заменено на новые 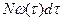 объектов. Из них на интервале
объектов. Из них на интервале 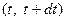 будут вновь заменены
будут вновь заменены 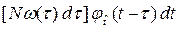 объектов. Суммируя по всем
объектов. Суммируя по всем 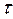 от 0 до
от 0 до 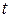 , получаем, что всего из числа уже отказавших (смененных) до момента времени
, получаем, что всего из числа уже отказавших (смененных) до момента времени 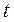 объектов на интервале вновь откажут
объектов на интервале вновь откажут 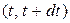
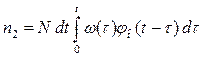 объектов.
объектов.
Тогда общее среднее количество отказов на интервале наработки 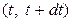 составит
составит
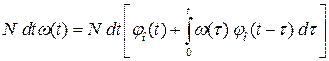 . (3.42)
. (3.42)
При сокращении на 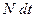 уравнение (3.42) принимает вид
уравнение (3.42) принимает вид
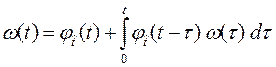 . (3.43)
. (3.43)
Таким образом, параметр потока отказов 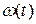 связан с плотностью распределения наработки между отказами
связан с плотностью распределения наработки между отказами 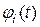 интегральным уравнением Вольтерра второго рода с разностным ядром [2-5]. Это уравнение не всегда удается решить в конечном виде. Если наработка между отказами-восстановлениями имеет показательное распределение, то из уравнения (3.43) следует, что если
интегральным уравнением Вольтерра второго рода с разностным ядром [2-5]. Это уравнение не всегда удается решить в конечном виде. Если наработка между отказами-восстановлениями имеет показательное распределение, то из уравнения (3.43) следует, что если 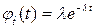 , то
, то 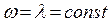 .
.
В технических заданиях на проектируемые объекты часто используют среднее значение
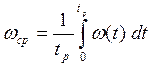 ,
,
где 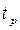 - технический ресурс или срок службы объекта.
- технический ресурс или срок службы объекта.
Для ординарных безпоследействия (Пуассоновских) потоков отказов вероятность безотказной работы объекта на интервале (t1 ,t2) выражается следующим образом:
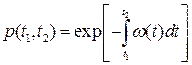 .
.
Если при 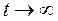 плотность распределения наработки до отказа
плотность распределения наработки до отказа 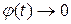 , то существует установившееся значение параметра потока отказов
, то существует установившееся значение параметра потока отказов
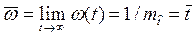 , (3.44)
, (3.44)
где 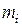 - средняя наработка на отказ восстанавливаемого объекта (в рассматриваемом случае совпадает со средней наработкой до отказа
- средняя наработка на отказ восстанавливаемого объекта (в рассматриваемом случае совпадает со средней наработкой до отказа 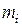 ).
).
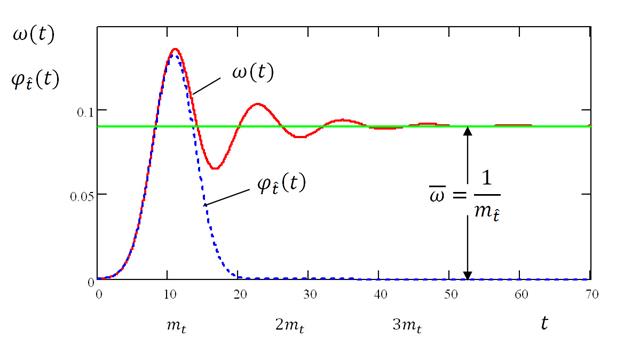
В общем случае средняя наработка 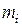 на отказ оценивается как отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Часто
на отказ оценивается как отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Часто 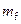 используется в качестве самостоятельного показателя надежности. Если наработка выражается в единицах времени, то может применяться термин «среднее время безотказной работы».
используется в качестве самостоятельного показателя надежности. Если наработка выражается в единицах времени, то может применяться термин «среднее время безотказной работы».
|
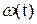 при нормальном распределении (
при нормальном распределении ( 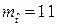 ,
, 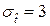 )
)
При нормальном распределении наработки между отказами параметр потока отказов
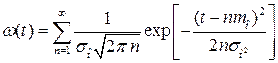 . (3.45)
. (3.45)
где 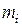 ,
, 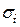 - среднее значение и среднее квадратическое отклонение наработки между отказами.
- среднее значение и среднее квадратическое отклонение наработки между отказами.
На рис. 3.6 показано, что значения параметра потока отказов совершают ряд колебаний, прежде чем станут равными 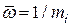 . Продолжительность этого колебательного процесса обратно пропорциональна среднему квадратическому отклонению наработки между отказами
. Продолжительность этого колебательного процесса обратно пропорциональна среднему квадратическому отклонению наработки между отказами 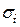 . Чем меньше
. Чем меньше 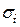 , тем определеннее отказы группируются около средних значений
, тем определеннее отказы группируются около средних значений 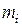 и тем большая суммарная наработка должна накопиться, прежде чем сравняют условия появления отказов. При
и тем большая суммарная наработка должна накопиться, прежде чем сравняют условия появления отказов. При 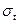 = 0 отказы происходят регулярно и установившееся значение
= 0 отказы происходят регулярно и установившееся значение 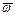 вообще не достигается.
вообще не достигается.
Таким образом, если рассматриваемый интервал наработки выбран достаточно далеко от начала эксплуатации объектов данного типа, то параметр потока отказов можно считать стационарным.
Дата добавления: 2016-09-26; просмотров: 3398;

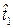
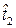
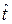
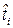
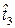
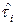
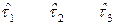
 (t)
(t)










