Показатели безотказности невосстанавливаемых объектов
Определение показателей безотказности невосстанавливаемых объектов проводится для простейшей модели невосстанавливаемого объекта: в момент начала работы 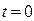 объект работоспособен; в случайный момент времени
объект работоспособен; в случайный момент времени 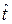 объект переходит в неработоспособное состояние, т.е. в этот момент происходит отказ. Для такой модели объекта его надежность полностью определяется безотказностью.
объект переходит в неработоспособное состояние, т.е. в этот момент происходит отказ. Для такой модели объекта его надежность полностью определяется безотказностью.
Случайную величину времени 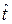 (наработку) до отказа невосстанавливаемых объектов в научно-технической литературе часто называют временем жизни объекта. Так как невозможно указать такие моменты времени, в которые отказ не был бы возможен, то наработка до отказа
(наработку) до отказа невосстанавливаемых объектов в научно-технической литературе часто называют временем жизни объекта. Так как невозможно указать такие моменты времени, в которые отказ не был бы возможен, то наработка до отказа 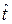 есть непрерывная случайная величина. Вероятностные характеристики случайной величины наработки до отказа
есть непрерывная случайная величина. Вероятностные характеристики случайной величины наработки до отказа 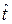 используются в качестве показателей безотказности невосстанавливаемых объектов.
используются в качестве показателей безотказности невосстанавливаемых объектов.
Вероятность события 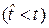 называется вероятностью отказа
называется вероятностью отказа 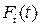 за время (наработку)
за время (наработку) 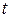 (или функцией «ненадежности» объекта).
(или функцией «ненадежности» объекта).
Вероятность отказа является функцией распределения случайной величины времени (наработки) до отказа и по определению имеет вид
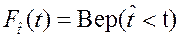 , (3.1)
, (3.1)
где Вер( 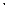 ) – символ вероятности события, записанного в круглых скобках;
) – символ вероятности события, записанного в круглых скобках;
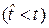 - событие, заключающееся в том, что случайное время (наработка)
- событие, заключающееся в том, что случайное время (наработка) 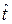 до отказа не превысит заданное
до отказа не превысит заданное 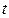 .
.
Так как неработоспособное и работоспособное состояния образуют полную группу несовместных событий, то вероятность безотказной работы за время (наработку) 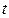 , или функция надежности
, или функция надежности
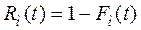 или
или 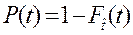 . (3.2)
. (3.2)
Отметим, что вероятность безотказной работы 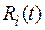 имеет смысл дополнительной функции распределения случайной величины
имеет смысл дополнительной функции распределения случайной величины 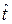 . Обозначение вероятности безотказной работы символом «
. Обозначение вероятности безотказной работы символом « 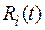 » является более информативным, так как индекс «
» является более информативным, так как индекс « 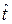 » определяет случайную величину, а аргумент
» определяет случайную величину, а аргумент 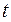 - заданную (детерминированную) наработку. В научно-технической литературе и нормативно-технической документации функция
- заданную (детерминированную) наработку. В научно-технической литературе и нормативно-технической документации функция 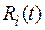 именуется функцией надежности или вероятностью безотказной работы и обозначается
именуется функцией надежности или вероятностью безотказной работы и обозначается 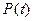 . Исходя из этого, в дальнейшем будет использовано обозначение вероятности безотказной работы или функции надежности
. Исходя из этого, в дальнейшем будет использовано обозначение вероятности безотказной работы или функции надежности 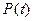 .
.
Под вероятностью безотказной работы 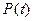 понимают вероятность того, что в пределах заданного времени (заданной наработки)
понимают вероятность того, что в пределах заданного времени (заданной наработки) 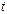 отказ не произойдет. Типичные зависимости вероятности безотказной работы
отказ не произойдет. Типичные зависимости вероятности безотказной работы 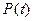 и вероятности отказа
и вероятности отказа 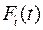 приведены на рис. 3.2.
приведены на рис. 3.2.
Основные свойства вероятности безотказной работы 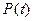 :
:
1) 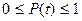 , так как
, так как 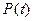 есть вероятность;
есть вероятность;
2) 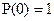 , т.е. вероятность безотказной работы определяется только для объектов, исправных в начальный момент времени их функционирования, и с этой точки зрения она является условной вероятностью (условием является исправное состояние в начальный момент времени);
, т.е. вероятность безотказной работы определяется только для объектов, исправных в начальный момент времени их функционирования, и с этой точки зрения она является условной вероятностью (условием является исправное состояние в начальный момент времени);
3)
|
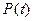 является монотонно убывающей функцией (при
является монотонно убывающей функцией (при 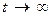 функция
функция 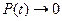 ).
).
|
| |

|
|
|
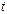 в формулах (3.1) – (3.2) обозначает не момент времени, а интервал времени. Так как для невосстанавливаемых объектов время (наработка) отсчитывается от начала эксплуатации, то интервал равен
в формулах (3.1) – (3.2) обозначает не момент времени, а интервал времени. Так как для невосстанавливаемых объектов время (наработка) отсчитывается от начала эксплуатации, то интервал равен 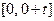 .
.
Оценка вероятности безотказной работы определяется по статистической информации об отказах
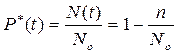 , (3.3)
, (3.3)
где 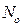 - число объектов, работоспособных в начальный момент
- число объектов, работоспособных в начальный момент
времени ( 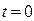 );
);
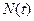 - число объектов, сохранивших работоспособное состояние
- число объектов, сохранивших работоспособное состояние
за заданную наработку 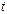 ;
;
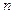 - число объектов, отказавших за заданную наработку
- число объектов, отказавших за заданную наработку 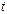 ;
;
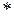 - символ оценки.
- символ оценки.
Точность определения оценки вероятности безотказной работы тем выше, чем больше объектов находится под наблюдением. При значительном числе объектов оценка статистической вероятности 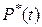 стремится к теоретической вероятности
стремится к теоретической вероятности 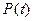 .
.
Несмотря на то, что любая из функций 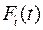 и
и 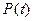 полностью характеризуют случайную величину
полностью характеризуют случайную величину 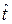 , в ряде случаев более удобными, простыми и наглядными оказываются некоторые дополнительные функциональные и числовые характеристики.
, в ряде случаев более удобными, простыми и наглядными оказываются некоторые дополнительные функциональные и числовые характеристики.
Так, весьма полезным вспомогательным инструментом исследования надежности является плотность распределения 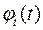 наработки до отказа, или дифференциальный закон распределения случайной величины
наработки до отказа, или дифференциальный закон распределения случайной величины 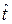 :
:
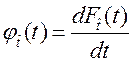 или
или 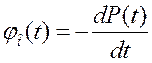 . (3.4)
. (3.4)
Основные свойства плотности распределения наработки до отказа:
1) функция 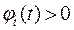 , так как она и есть производная от монотонно возрастающей функции
, так как она и есть производная от монотонно возрастающей функции 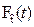 ;
;
2) 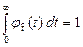 ;
;
3) Размерность 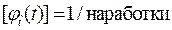 , например, 1/ч.
, например, 1/ч.
Кроме указанных показателей в теории надежности и в практике эксплуатации в качестве единичных показателей безотказности невосстанавливаемых объектов используются числовые характеристики распределения наработки до отказа: средняя наработка до отказа 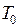 ; интенсивность отказов
; интенсивность отказов 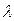 ; гамма-процентная наработка до отказа
; гамма-процентная наработка до отказа 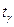 .
.
Средняя наработка до отказа 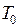 определяется как математическое ожидание наработки объекта до отказа, т.е.
определяется как математическое ожидание наработки объекта до отказа, т.е.
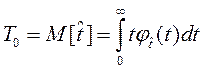 , (3.5)
, (3.5)
где 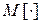 - символ математического ожидания.
- символ математического ожидания.
Выражение (3.4) с учетом (3.1) и (3.3) преобразуется к виду
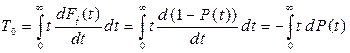 .
.
Если обозначить 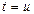 и
и 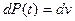 , следовательно,
, следовательно, 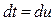 и
и 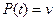 , то полученный интеграл может быть взят по частям
, то полученный интеграл может быть взят по частям 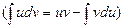 :
:
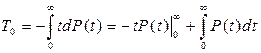 .
.
Так как 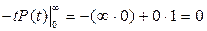 , то
, то
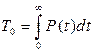 .(3.6)
.(3.6)
Из анализа формулы (3.6) и графика 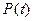 (см. рис. 3.2) следует, что средняя наработка до отказа
(см. рис. 3.2) следует, что средняя наработка до отказа 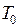 численно равна площади под кривой
численно равна площади под кривой 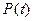 на интервале
на интервале 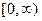 .
.
Оценка средней наработки до отказа (3.6) по статистическим данным зависит от плана испытаний и закона распределения наработки до отказа [1-5].
Если испытания ведутся до отказа всех объектов, то оценка средней наработки до отказа определяется по формуле
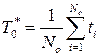 , (3.7)
, (3.7)
где 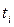 - наработка до отказа i-го объекта.
- наработка до отказа i-го объекта.
В практике эксплуатации, как правило, известны данные об отказах за определенное время 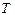 , когда из
, когда из 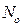 объектов, имеющихся к началу эксплуатации, откажет только n. Тогда для оценки средней наработки до отказа для случая, когда частота возникновения отказов постоянна, следует пользоваться соотношением
объектов, имеющихся к началу эксплуатации, откажет только n. Тогда для оценки средней наработки до отказа для случая, когда частота возникновения отказов постоянна, следует пользоваться соотношением
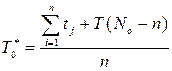 .
.
Интенсивностью отказов 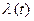 называется условная плотность вероятности возникновения отказа объекта в момент времени (наработки)
называется условная плотность вероятности возникновения отказа объекта в момент времени (наработки) 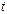 , определяемая при условии, что до рассматриваемого момента времени отказ не возник.
, определяемая при условии, что до рассматриваемого момента времени отказ не возник.
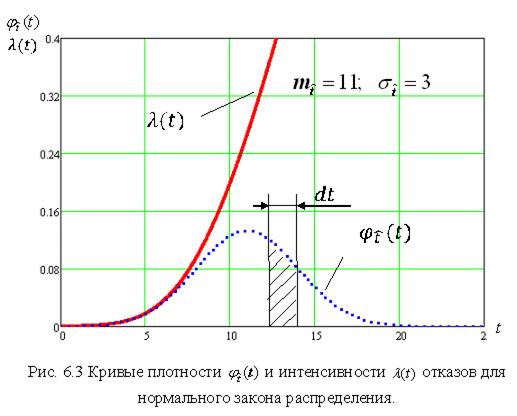
На рис.3.3 показана плотность распределения наработки на отказ для нормального закона распределения, на котором отмечен заданный момент времени t и элементарное приращение времени (наработки) 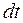 , примыкающее к моменту времени t. Элементарное значение безусловной вероятности отказа на этом приращении времени в соответствии с (3.4) равно
, примыкающее к моменту времени t. Элементарное значение безусловной вероятности отказа на этом приращении времени в соответствии с (3.4) равно 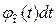 , как это показано на рис.3.3. Элементарное значение условной вероятности отказа на этом же отрезке, определяемое при условии, что в момент времени
, как это показано на рис.3.3. Элементарное значение условной вероятности отказа на этом же отрезке, определяемое при условии, что в момент времени 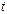 отказ не возник, равно
отказ не возник, равно 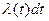 . Из теории вероятностей известно (2.5), что безусловная вероятность
. Из теории вероятностей известно (2.5), что безусловная вероятность 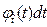 равна произведению условной вероятности
равна произведению условной вероятности 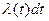 на вероятность условия
на вероятность условия 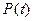 , то есть
, то есть
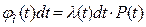 . (3.11)
. (3.11)
|
Сокращения левой и правой частей полученного выражения (3.11) на 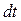 дает уравнение связи интенсивности отказов с (безусловной) плотностью вероятности отказа
дает уравнение связи интенсивности отказов с (безусловной) плотностью вероятности отказа 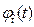
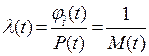 , (3.12)
, (3.12)
где 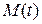 - отношение Миллса [2,18].
- отношение Миллса [2,18].
Интенсивность отказов есть условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени dt при условии, что до этого момента отказ не возник. Подстановка (3.2) и (3.4) в (3.12) приводит к выражению
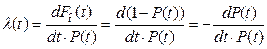 ,
,
Преобразование которого дает уравнение связи вероятности безотказной работы 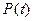 объекта с интенсивностью отказа
объекта с интенсивностью отказа 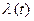 :
:
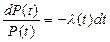 . (3.13)
. (3.13)
Интегрирование полученного уравнения (3.13) в пределах от 0 до 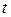 , приводит к результату
, приводит к результату 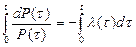 ,
,
где 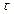 - аргумент (по смыслу наработка), откуда
- аргумент (по смыслу наработка), откуда
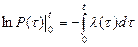 .
.
Так как 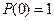 и
и 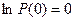 , то
, то 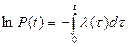 , то после интегрирования получаем основную формулу надежности для невосстанавливаемых объектов
, то после интегрирования получаем основную формулу надежности для невосстанавливаемых объектов
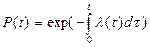 . (3.14)
. (3.14)
Интенсивность отказа 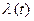 характеризует не интервальную, а локальную или мгновенную безотказность объекта в момент времени
характеризует не интервальную, а локальную или мгновенную безотказность объекта в момент времени 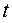 и является показателем безотказности, зависящим от времени (наработки)
и является показателем безотказности, зависящим от времени (наработки) 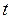 .
.
Экспериментально установлено, что практически для всех технических объектов график зависимости интенсивности отказов от наработки имеет вид, представленный на рис. 3.4.
| |
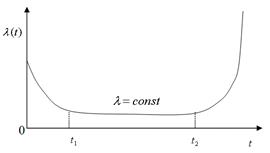
Рис. 3.4. Зависимость интенсивности отказов от времени (наработки)
Интервал времени (наработка) 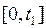 соответствует периоду приработки, на котором выявляются, в основном, конструктивные и производственные отказы, чаще всего относящиеся к внезапным. По мере приработки и устранения отказов интенсивность отказов уменьшается. Продолжительность этого периода зависит от вида объекта и интенсивности отказов его элементов. Продолжительность этого периода может быть уменьшена в результате «тренировки» объекта в заводских условиях.
соответствует периоду приработки, на котором выявляются, в основном, конструктивные и производственные отказы, чаще всего относящиеся к внезапным. По мере приработки и устранения отказов интенсивность отказов уменьшается. Продолжительность этого периода зависит от вида объекта и интенсивности отказов его элементов. Продолжительность этого периода может быть уменьшена в результате «тренировки» объекта в заводских условиях.
Интервал времени (наработки) 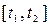 соответствует периоду нормальной эксплуатации объекта. На этом участке интенсивность отказов практически постоянна. Отказы этого периода относятся как к внезапным, так и к постепенным. Значение интенсивности отказов здесь может быть снижено за счет своевременного и качественного процесса контроля, отработки и технического обслуживания. Следует стремиться, чтобы объект использовался по назначению только в период нормальной эксплуатации.
соответствует периоду нормальной эксплуатации объекта. На этом участке интенсивность отказов практически постоянна. Отказы этого периода относятся как к внезапным, так и к постепенным. Значение интенсивности отказов здесь может быть снижено за счет своевременного и качественного процесса контроля, отработки и технического обслуживания. Следует стремиться, чтобы объект использовался по назначению только в период нормальной эксплуатации.
Интервал времени (наработка) 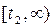 характеризуется тем, что из-за усиления процессов старения и износа интенсивность отказов возрастает. Этот участок называется участком старения.
характеризуется тем, что из-за усиления процессов старения и износа интенсивность отказов возрастает. Этот участок называется участком старения.
По статистическим данным оценка интенсивности отказов может быть определена из соотношения
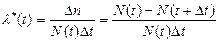 , (3.15)
, (3.15)
где 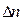 - число отказавших объектов на интервале времени (наработки)
- число отказавших объектов на интервале времени (наработки) 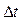 ;
;
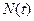 ,
, 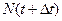 - число объектов, работоспособных соответственно к моментам времени
- число объектов, работоспособных соответственно к моментам времени 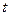 и
и 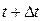 .
.
Безотказность объектов 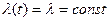 характеризует надежность невосстанавливаемых объектов периода нормальной эксплуатации и описывается экспоненциальным законом распределения времени (наработки)
характеризует надежность невосстанавливаемых объектов периода нормальной эксплуатации и описывается экспоненциальным законом распределения времени (наработки) 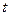 .
.
Для экспоненциального закона функциональные и числовые характеристики имеют вид (2.23), (2.24), (2.25):
вероятность безотказной работы за время (наработку) 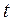
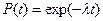 . (3.16)
. (3.16)
вероятность отказа за время (наработку) 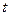
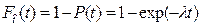 ; (3.17)
; (3.17)
плотность распределения наработки до отказа 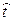
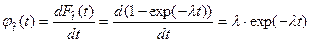 ; (3.18)
; (3.18)
средняя наработка до отказа
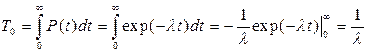 , (3.19)
, (3.19)
Что совпадает с выражением (2.13) для модели внезапных отказов.
Из (3.16) с учетом (3.19) следует еще одна формула для вероятности безотказной работы
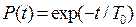 , (3.20)
, (3.20)
которая также совпадает с формулой (2.21) для модели внезапных отказов.
Гамма-процентной наработкой до отказа 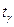 называется наработка, в течение которой отказ объекта не возникнет с вероятностью
называется наработка, в течение которой отказ объекта не возникнет с вероятностью 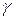 , выраженной в процентах.
, выраженной в процентах.
Для произвольного закона распределения времени (наработки) до отказа гамма-процентная наработка до отказа 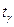 может быть получена двумя способами:
может быть получена двумя способами:
численным интегрированием уравнения (3.14) при условиях: верхний предел интегрирования равен 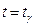 , а вероятность безотказной работы -
, а вероятность безотказной работы - 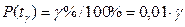 ;
;
графически (см. рис. 3.2): входом в график является вероятность 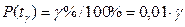 , а выходом – гамма-процентная наработка до отказа
, а выходом – гамма-процентная наработка до отказа 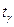 .
.
Для экспоненциального закона распределения гамма-процентная наработка до отказа 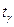 может быть получена из (3.14) при условиях:
может быть получена из (3.14) при условиях: 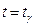 и
и 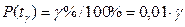 , т.е.
, т.е. 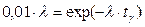 , или окончательно
, или окончательно
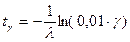 . (3.21)
. (3.21)
Пример 3.1. В эксплуатации находятся 50 однотипных невосстанавливаемых объектов. В течение одного года в неработоспособное состояние вследствие отказов перешли 30 объектов. Рассчитать оценки показателей безотказности.
Решение:
1. Число работоспособных объектов 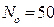 ; число неработоспособных объектов
; число неработоспособных объектов 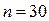 ; интервал времени T = 1 год = 24 365 = 8760 часов.
; интервал времени T = 1 год = 24 365 = 8760 часов.
2. Наработки до отказа всех объектов вносятся в таблицу 3.1 (в предположении, что объекты используются на участке нормальной эксплуатации и интенсивность (частота) отказов постоянна 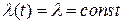 ).
).
Таблица 3.1.
| Номер объекта i | … | |||||
Наработка до отказа 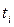 , ч. , ч.
| … |
3. Расчет оценок показателей безотказности в соответствии с формулами (3.6), (3.12) и (3.20) производиться следующим образом:
вероятности безотказной работы за один год
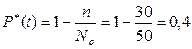 ;
;
средней наработки до отказа
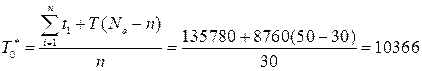 ч.
ч.
интенсивности отказов
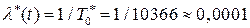 1/ч.
1/ч.
Пример 3.2. Рассчитать показатели безотказности электродвигателя в течение наработки t=500 ч, для которого интенсивность отказов 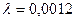 1/ч.
1/ч.
Решение:
1. Средняя наработка до отказа
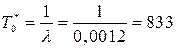 ч.
ч.
2. Вероятность безотказный работы в течение наработки 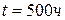
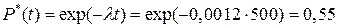 .
.
3. Гамма-процентная наработка до отказа для уровня 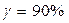
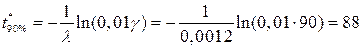 ч.
ч.
Дата добавления: 2016-09-26; просмотров: 5339;

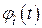 и интенсивности
и интенсивности 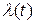 отказа для нормального закона распределения
отказа для нормального закона распределения










