Функция готовности объектов с конечным временем восстановления
Время восстановления 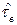 зависит как от свойства надежности самого объекта, так и характеристик обслуживающего персонала, наличия ЗИП, характеристик оснащенности средствами контроля и диагностики организационно-технической системы, в состав которой входит объект и т.д. Следовательно, при формировании показателей надежности объектов с конечным временем восстановления необходимо учитывать как показатели надежности объектов, так и показатели свойств указанной организационно-технической системы.
зависит как от свойства надежности самого объекта, так и характеристик обслуживающего персонала, наличия ЗИП, характеристик оснащенности средствами контроля и диагностики организационно-технической системы, в состав которой входит объект и т.д. Следовательно, при формировании показателей надежности объектов с конечным временем восстановления необходимо учитывать как показатели надежности объектов, так и показатели свойств указанной организационно-технической системы.
В общем случае модель восстанавливаемого объекта с конечным случайным временем восстановления формируется следующим образом: в момент времени 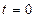 объект работоспособен, проработав случайное время
объект работоспособен, проработав случайное время 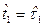 , объект переходит в неработоспособное состояние, то есть возникает первый отказ, затем в течение случайного времени
, объект переходит в неработоспособное состояние, то есть возникает первый отказ, затем в течение случайного времени 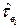 происходит восстановление объекта, в результате чего он полностью восстанавливается до состояния, в котором он находился в момент
происходит восстановление объекта, в результате чего он полностью восстанавливается до состояния, в котором он находился в момент 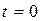 . Далее, проработав некоторое случайное время
. Далее, проработав некоторое случайное время 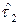 , объект второй раз переходит в неработоспособное состояние, то есть в случайный момент времени
, объект второй раз переходит в неработоспособное состояние, то есть в случайный момент времени 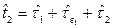 возникает второй отказ, затем за случайное время
возникает второй отказ, затем за случайное время 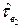 объект вновь восстанавливается до первоначального состояния.
объект вновь восстанавливается до первоначального состояния.
При этом предполагается, что контроль работоспособности объекта является непрерывным и полностью достоверным.
Описанная выше модель функционирования восстанавливаемого объекта с конечным временем восстановления представлена на рис. 3.7.
|
|
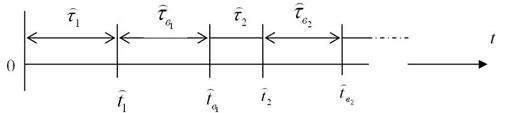
Рис. 3.7 Модель функционирования восстанавливаемого объекта с конечным временем восстановления.
Если объект имеет экспоненциальное распределение времени безотказной работы, а знание какой-либо предыстории объекта не представляет большой ценности для предсказания ее поведения в будущем, то представленный на рис. 3.7 процесс может быть описан марковским процессом [2,18,21]. В этом случае случайные величины времени 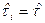 между отказами и времени
между отказами и времени 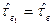 восстановления являются независимыми случайными величинами, распределенными по экспоненциальным законам, то есть потоки отказов и восстановлений являются простейшими потоками. При этом поток отказов характеризуется параметром потока (интенсивностью) отказов
восстановления являются независимыми случайными величинами, распределенными по экспоненциальным законам, то есть потоки отказов и восстановлений являются простейшими потоками. При этом поток отказов характеризуется параметром потока (интенсивностью) отказов 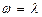 или наработкой на отказ
или наработкой на отказ 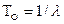 , а поток восстановлений – параметром потока (интенсивностью) восстановления
, а поток восстановлений – параметром потока (интенсивностью) восстановления 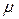 или средним временем восстановления
или средним временем восстановления 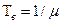 .
.
Для модели (см. рис. 3.7) функционирования восстанавливаемого объекта с конечным временем восстановления в качестве показателя надежности используются функция готовности 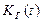 или коэффициент готовности
или коэффициент готовности 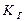 .
.
 Функция готовности
Функция готовности 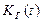 представляет собой вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени (наработки)
представляет собой вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени (наработки) 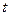 .
.

Рис. 3.8. Граф состояний восстанавливаемого объекта.
Для модели, представленной на рис.3.7, граф состояний восстанавливаемого объекта показан на рис.3.8. Этот граф имеет два возможных состояния: работоспособное 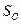 с вероятностью пребывания в нем
с вероятностью пребывания в нем 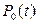 и неработоспособное
и неработоспособное 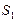 с вероятностью пребывания в нем
с вероятностью пребывания в нем 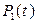 .При появлении отказа объект из состояния
.При появлении отказа объект из состояния 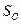 переходит в состояние
переходит в состояние 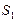 с интенсивностью
с интенсивностью 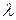 . После завершения восстановления объект возвращается в работоспособное состояние
. После завершения восстановления объект возвращается в работоспособное состояние 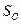 с интенсивностью восстановления
с интенсивностью восстановления 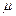 .
.
Граф состояний на рис. 3.8 описывается системой дифференциальных уравнений Колмогорова [2-9, 17-22]:
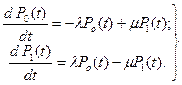 (3.46)
(3.46)
Так как состояния 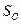 и
и 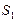 образуют полную группу несовместимых событий, то нормирующим условием для системы (3.46) будет равенство
образуют полную группу несовместимых событий, то нормирующим условием для системы (3.46) будет равенство
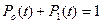 , (3.47)
, (3.47)
что позволяет уменьшить на единицу число уравнений (3.46).
Начальные условия для дифференциальных уравнений (3.46) составляют
при 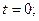
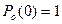 и
и 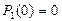 . (3.48)
. (3.48)
Решение первого из уравнений (3.46) с учетом нормирующего условия (3.47) и начальных условий (3.48) позволяет получить выражение для функции готовности 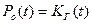 . Так, из (3.47) следует
. Так, из (3.47) следует 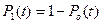 . Подстановка этого выражения в первое уравнение системы (3.46) дает следующий результат
. Подстановка этого выражения в первое уравнение системы (3.46) дает следующий результат
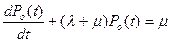 . (3.49)
. (3.49)
Полученное выражение (3.49) представляет собой неоднородное дифференциальное уравнение с постоянной правой частью.
Общее решение этого уравнения (3.49) равно сумме его однородного и неоднородного решений.
Чтобы найти решение неоднородного уравнения при условии существования предельной вероятности 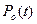 , необходимо приравнять нулю производную левой части выражения (3.49), то есть
, необходимо приравнять нулю производную левой части выражения (3.49), то есть
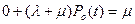 ,
,
откуда
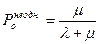 . (3.50)
. (3.50)
Решение однородного уравнения отыскивается из исходного уравнения (3.49) путем приравнивания нулю его правой части 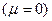
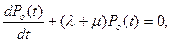
откуда
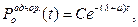 (3.51)
(3.51)
где C – постоянная интегрирования.
Постоянная интегрирования C может быть получена из общего решения уравнения (3.51) с учетом начальных условий (3.48).
Так общее решение уравнения (3.49) будет равно
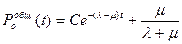 , (3.52)
, (3.52)
которое при 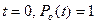 преобразуется к виду
преобразуется к виду
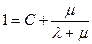 ,
,
откуда
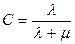 . (3.53)
. (3.53)
Подстановка (3.53) в формулу (3.52) дает окончательное выражение для функции готовности, которое определяется следующим образом
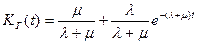 . (3.54)
. (3.54)
С учетом того, что среднее время безотказной работы объекта 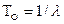 , а среднее время восстановления
, а среднее время восстановления 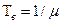 , то функция готовности (3.54) примет вид
, то функция готовности (3.54) примет вид
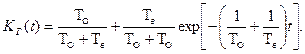 (3.55)
(3.55)
В формулах (3.54) и (3.55) интенсивность отказов 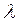 и наработка на отказ
и наработка на отказ 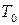 являются показателями безотказности, а интенсивность восстановления
являются показателями безотказности, а интенсивность восстановления 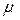 и среднее время восстановления
и среднее время восстановления 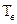 являются показателями ремонтопригодности. Следовательно, функция готовности (3.54), (3.55) определяется показателями двух свойств надежности [1-5]: безотказности и ремонтопригодности, являясь комплексным показателем надежности ОТС.
являются показателями ремонтопригодности. Следовательно, функция готовности (3.54), (3.55) определяется показателями двух свойств надежности [1-5]: безотказности и ремонтопригодности, являясь комплексным показателем надежности ОТС.
Анализ функций (3.54), (3.55) показывает, что при 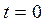 функция готовности равна единице
функция готовности равна единице 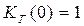 . Предельное значение функции готовности (при
. Предельное значение функции готовности (при 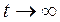 ) называется коэффициентом готовности, то есть
) называется коэффициентом готовности, то есть
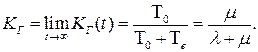 (3.56)
(3.56)
При 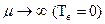 , что соответствует мгновенному восстановлению, первое слагаемое правой части выражения (3.55) стремится к единице, а второе слагаемое стремится к нулю, следовательно,
, что соответствует мгновенному восстановлению, первое слагаемое правой части выражения (3.55) стремится к единице, а второе слагаемое стремится к нулю, следовательно, 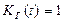 , то есть объект, будет постоянно находиться в работоспособном состоянии. Отсюда следует, что одним из главных путей повышения надежности восстанавливаемых объектов является сокращение среднего времени восстановления
, то есть объект, будет постоянно находиться в работоспособном состоянии. Отсюда следует, что одним из главных путей повышения надежности восстанавливаемых объектов является сокращение среднего времени восстановления 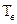 , то есть улучшение показателя ремонтопригодности в ОТС.
, то есть улучшение показателя ремонтопригодности в ОТС.
При 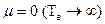 , что соответствует низким значениям показателей ремонтопригодности или слабой подготовке персонала, из формул (3.54), (3.55) следует, что значение функции готовности будет определяться только функцией надежности невосстанавливаемого объекта.
, что соответствует низким значениям показателей ремонтопригодности или слабой подготовке персонала, из формул (3.54), (3.55) следует, что значение функции готовности будет определяться только функцией надежности невосстанавливаемого объекта.
|
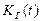 при различных значениях показателей надежности
при различных значениях показателей надежности 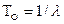 и восстанавливаемости
и восстанавливаемости 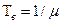 приведены на рис. 3.9.
приведены на рис. 3.9.
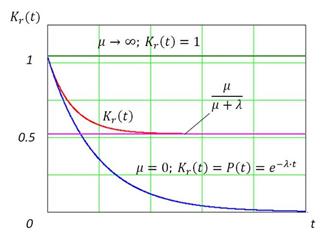
Рис. 3.9. Графики функции готовности
Как правило, на практике функция готовности 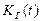 стремится к стационарному значению, то есть к коэффициенту готовности
стремится к стационарному значению, то есть к коэффициенту готовности 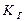 за наработку, меньшую наработке на отказ, что позволяет использовать его в качестве показателя надежности восстанавливаемых объектов [1,2,4,6].
за наработку, меньшую наработке на отказ, что позволяет использовать его в качестве показателя надежности восстанавливаемых объектов [1,2,4,6].
Дата добавления: 2016-09-26; просмотров: 4575;



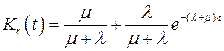 , где
, где 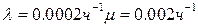 .
.










