Модель параметрической надежности объекта при нескольких параметрах, характеризующих работоспособность его систем и элементов.

В целом параметрическая надежность сложных объектов, например, параметрическая надежность двигательной установки летательного аппарата (ЛА), будет определяться векторами положения и скорости в момент выключения двигателя, определяющих расчетную дальность L ЛА (его основной выходной параметр), которая является функцией ряда его бортовых параметров x₁(t), x₅(t), …, x_n(t), определяющих надежность ЛА, то есть [8,9]

L (x₁(t), x₂(t),…, x_n(t)). (2.72)

Здесь L является основным выходным параметром ЛА, составляющими которого являются выходные параметры x₁(t), x₅(t), …, x_n(t) ряда бортовых систем и элементов объекта.

При этом

L = L₀ + ∆L ,

где L₀ – расчетное значение основного выходного параметра, определяемое номинальными значениями выходных параметров x₁(t), x₅(t), …, x_n(t) систем и элементовобъекта;

∆L – приращение выходного параметра объекта, обусловленное вариациями параметров x₁(t), x₅(t), …, x_n(t);

n – число выходных параметров систем и элементов, вносящих вклад в изменение ∆L выходного рабочего параметра объекта.

Изменение ∆l_i выходного параметра объекта L₀ за счет вариации параметра x_i(t) входящей в его состав i-ой системы элемента составит:

∆l_i = L₀ – L_i .

Тогда изменение рабочего выходного параметра объекта за счет вариации всех параметров x₁(t), x₅(t), …, x_n(t) совместноможет быть определено алгебраической суммой:

∆L = 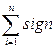∆l_i , (2.73)

где sign – сигнатура числа ∆l_i , т.е.

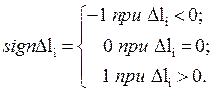
В силу предполагаемых монотонности и непрерывности функции (2.72) дополнительное от вариации ∆x_i i-ого параметра x_i(t) изменение выходного рабочего параметра ∆l_i объекта можно представить разложением в ряд Тейлора по степеням ∆x_i [2-5,16,18]:

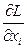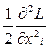∆l_i = ∆x_i + ∆x²_i + … (2.74)

Тогда с учетом (2.72) суммарное изменение ∆L выходного параметра L, обусловленное вариациями всех параметров систем и элементов объекта может быть определено следующим образом:

∆L = 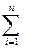( 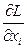∆x_i + 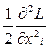∆x²_i + …) (2.75)

На основе выражений (2.74), (2.75) относительное изменение α_i выходного рабочего параметра объекта под влиянием входного параметра x_i(t) i-ого элемента объекта примет вид:

α_i = 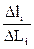= 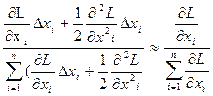. (2.76)

При этом производные высшего порядка не учитываются, поскольку они слабо влияют на величину α_i, которая не зависит от времени t, если случайные функции x₁(t), x₅(t), …, x_n(t) являются линейными, или близки к ним.

Легко видеть, что параметры α₁, α_5, …, α_n представляют собой коэффициенты чувствительности изменения выходного рабочего параметра объекта к вариациям выходных параметров бортовых систем и элементов объекта.

На практике ограничения накладываются не только на отклонение ∆L выходного параметра объекта, но и на параметры x₁(t), x₂(t), …, x_n(t), при которых обеспечивается его работоспособность, то есть

x_i(t) Î {x_i}, i = 1, 2, …, n , (2.77)

где {x_i} – область допустимых значений i-ого параметра.

В этом случае отклонение i-ого параметра за пределы установленной области (2.74) или обусловленное вариацией этого параметра отклонение выходного рабочего параметра объекта за пределы допуска, т.е. ΔL_iÏΔL₀ при x₁(t)Î{x_i} классифицируется как нарушение работоспособности (отказ) объекта.

Тогда вероятность выхода рабочего параметра L за пределы допуска под воздействием вариации i-ого параметра с учетом формулы (2.76), т.е. “веса” i-ого параметра x_i(t), записывается следующим образом:

q_i (t) = α_i*q_i[x_i(t)], (2.78)

где q_i [x_i(t)] – вероятность выхода i-ого параметра за пределы допуска за время работы t.

Тогда эти вероятности 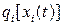с учетом формы допуска могут быть представлены в виде:

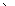
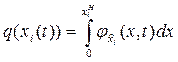- при одностороннем

нижнем допуске x_i^H ≤ x_i ≤ ∞,

(2.79)

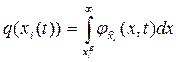- при одностороннем

верхнем допуске 0 < x_i ≤ x_i^В,

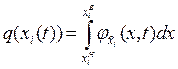- при двухстороннем

допуске x_i^H ≤ x_i ≤ x_i^В,

где x_i^H, x_i^В – нижняя и верхняя границы поля допуска случайной величины 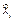(t).

С учетом выражений (2.78) и (2.79) вероятность безотказной работы объекта под влиянием i-ого параметра составит:

p_i(t) = 1 - α_iq_i(t), (2.80)

где α_i*- статистическое значение коэффициента α_i

Тогда параметрическая надежность объекта в целом с учетом (2.78) будет равна:

P(t) = 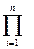[1 - α_iq_i(t)] . (2.81)

Таким образом, параметрическая надежность объекта сводится к вычислению оценок α_i* коэффициентов α_i и вероятностей q_i (t).

При этом для вычисления коэффициентов чувствительности α_i нет необходимости знать оператор L, получение которого сопряжено с большими трудностями. Достаточно располагать лишь статистическими данными о параметрических отказах элементов (2.76) объекта при его отработке. В этом случае оценки коэффициентов α_i определяются следующим образом:

α_i*= 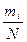, (2.80)

где m_i – количество отказов объекта вследствие ухода его i-ого параметра за пределы допуска (2.79);

N – общее количество отказов объекта, зафиксированное по причинам выхода за пределы допусков его систем и элементов.

Значения допусков (2.77) и (2.79) на параметры x_i(t) систем иэлементов объекта и коэффициентов чувствительности (2.76) могут быть получены и определены на этапе заводских и приемо-сдаточных испытаний [1-5].

Таким образом, управляя значениями допусков x_i^H, x_i^В на выходные параметры (2.77), (2.79) элементов объекта можно обеспечить требуемое значение показателя параметрической надежности (2.81) объекта в целом.