Поле равномерно заряженного проводника конечной длины

До сих пор мы рассматривали примеры электростатических полей, которые сводились к полям одного или нескольких отдельных точечных зарядов. В данном параграфе и двух последующих будут приведены примеры полей, создаваемых непрерывным распределением зарядов. Пусть нам дан бесконечно тонкий, равномерно заряженный проводник конечной длины L (рис.2.15) с линейной плотностью заряда s. Требуется найти потенциал и напряженность электрического поля в любой точке пространства вне проводника. Как и в задаче о бесконечно тонком, равномерно заряженном проводнике бесконечной длины (см.§2.4) задача имеет цилиндрическую симметрию. Ось симметрии бесконечного порядка проходит через заряженный проводник. В силу симметрии задача сводится к определению характеристик двумерного поля в плоскости, содержащей ось симметрии. На рис.2.15 введены следующие обозначения: х и у – оси координат; точка М₁ с координатами (x₁, y₁) и точка М₂ с координатами (x₂, y₂) соответствуют началу и концу бесконечно тонкого проводника; произвольная точка М с координатами (x, y) – точка в которой рассчитываются потенциал и напряженность поля; d – длина перпендикуляра, опущенного из расчетной точки М на нить или ее продолжение; dx – текущий бесконечно малый элемент нити; -х – расстояние от начала координат до элемента dx. Остальные обозначения приведены на рис.2.5. Заряд бесконечно малого отрезка dx равен dq=s×dx. Этот заряд можно считать точечным зарядом. В точке М он создает потенциал и напряженность

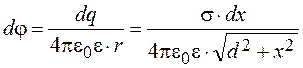(2.74)

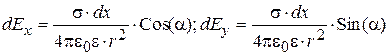(2.75)

Произведем замены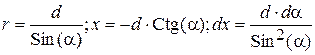

Тогда

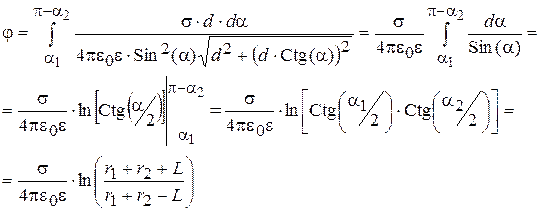(2.76)

Последнее преобразование проведено по формуле Мальвейде.

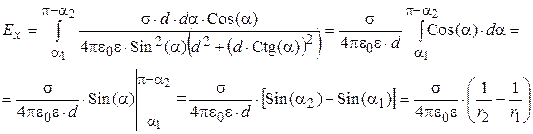(2.77)

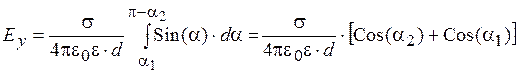(2.78)

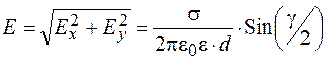(2.79)

Из соотношения (2.76) следует, что эквипотенциальные линии с j=const должны удовлетворять условию r₁+r₂ = const. Из курса математики известно, что такая фигура, для каждой точки которой сумма расстояний от двух заданных точек постоянна, называется эллипс. Сами точки конца проводника М₁ и М₂ расположены в фокусах. В пространстве эквипотенциальные поверхности представляют собой конфокальные эллипсоиды вращения. Поскольку силовые линии всегда перпендикулярны эквипотенциальным поверхностям, то в плоскости они представляют собой конфокальные гиперболы, а в пространстве конфокальные гиперболоиды вращения. Нормаль к эллипсу в произвольной точке М делит пополам угол между радиус-векторами, проведенными из фокусов в М, что также следует из (2.79). Приведем явный вид некоторых переменных в координатной форме

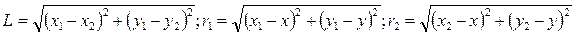
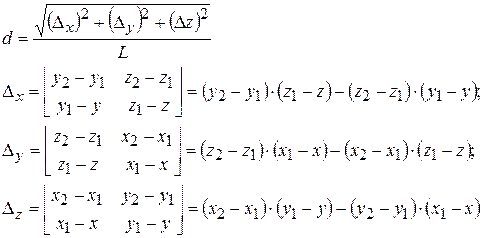(2.80)

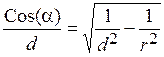(2.81)

В выражении (2.80) расстояние (d) между расчетной точкой и прямой, содержащей заряженный проводник, приведено для трехмерного пространства. В плоском поле все координаты z следует принять равными нулю. Как будет показано в следующем разделе, при приближенных расчетах электрических полей методом эквивалентных зарядов реальную систему электродов заменяют набором пробных зарядов, основными из которых являются точечные, линейные и кольцевые заряды. В таких расчетах используются формулы в координатной форме. Наиболее простой вид выражения для напряженности поля будет, если точка М лежит на оси симметрии. Тогда радиальные составляющие напряженности равны нулю (Е_у=0), а общая напряженность поля вычисляется по формуле (2.77). На концах заряженной нити или r₁=0 или r₂=0. Тогда напряженность обращается в бесконечность. Из этого результата следует, что максимальная напряженность на концах нити. Как будет показано далее в этом разделе, напряженность на концах заряженного отрезка является конечной величиной при учете реальной толщины проводника.