Поле кольцевого заряда
Пусть нам дан проводник в форме окружности (кольца) с центром в точке 0 и радиусом R, заряженный равномерно с линейной плотностью заряда t. Система имеет ось симметрии С¥, совпадающую с осью х рис.2.16. Задача о параметрах поля в пространстве вырождается, как и предыдущем параграфе, в задачу на плоскости, содержащей ось симметрии. Простые аналитические выражения параметров поля получаются только для точек, лежащих на оси симметрии. Из соображений симметрии следует, что вектор напряженности в точках, лежащих на оси симметрии, имеет только осевую составляющую (Е = Ех). Определим потенциал и напряженность поля в произвольной точке М, на оси симметрии. На заряженном кольце выделим бесконечно малый участок с зарядом dq и длиной R×dq, который можно принять за точечный заряд. Величина заряда равна dq = t×R×dq. Расстояние от этого точечного заряда до расчетной точки М обозначим символом r, а угол между r и осью х символом a (Sina =R/r).

Потенциал и напряженность электростатического поля, которые создает этот элементарный заряд, равны:
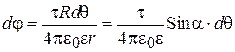 (2.82)
(2.82)
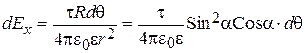 (2.83)
(2.83)
Для получения параметров поля кольца следует взять интеграл по всей длине кольца. Обозначив угол до элемента кольца q, пределы интегрирования получим от q=0 до q=2p. Расстояния от любого элемента кольца до точки на оси будут равны между собой (r). Равны также и углы между r и х (угол a). После интегрирования получаем:
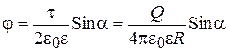 (2.84)
(2.84)
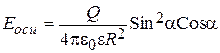 , (2.85)
, (2.85)
где Q = 2pR×t - заряд кольца. Максимальное (по модулю) значение потенциала наблюдается при значении Sina=1, т.е угол a=90°, что соответствует точке 0 в центре кольца. Максимальное значение напряженности поля соответствует экстремуму функции f = Sin2a×Cosa. Должно выполняться соотношение 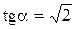 . Это условие выполняется в точке оси, отстоящей от цен-
. Это условие выполняется в точке оси, отстоящей от цен-
тра кольца (точка 0) на величину 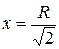 . Минимальное значение напряженности (Е = 0) соответствует центру кольца. Значение тангенса
. Минимальное значение напряженности (Е = 0) соответствует центру кольца. Значение тангенса 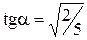
соответствует точке перегиба функции f. Точка перегиба отстоит от центра
кольца на величину 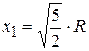 .
.
Дата добавления: 2016-09-26; просмотров: 2344;











