Поле заряженного диска

Пусть нам дан не проводящий диск с центром в точке 0 и радиусом R, заряженный равномерно с поверхностной плотностью заряда s = Q/(2pR²). Система, как и в двух предыдущих параграфах, имеет ось симметрии С_¥, совпадающую с осью х рис.2.17. Задача о параметрах поля в пространстве вырождается в задачу на плоскости, содержащей ось симметрии. Наличие плоскости симметрии, совпадающей с плоскостью диска, и взаимно-перпендикулярных плоскостей симметрии, содержащих ось С_¥, позволяет, рассчитав параметры поля в четвертой части плоскости, описать поле в пространстве. Как и в предыдущем параграфе будем рассчитывать параметры поля только для точек, лежащих на оси симметрии, для которых получаются компактные аналитические выражения. Обозначения приведены на рис.2.17. Представим заряженный диск как совокупность вложенных друг в друга

тонких колец толщиной dy. Пусть радиус такого произвольно выделенного кольца равен у. Определим потенциал и напряженность от этого кольца в точке М, лежащей на оси симметрии на расстоянии х от центра диска (кольца). Для этого воспользуемся формулами (2.84), (2.85), выведенными в предыдущем параграфе. Заменим в этих формулах линейную плотность заряда t на поверхностную плотность s, j на dj, Е_оси на dЕ_оси, R на y = x×tga, Q на dQ= s×2py×dy (dy =x×da/Cos²a):

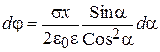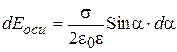, (2.86)

Для получения параметров поля диска следует провести интегрирование выражений (2.86) по углу a в пределах от a = 0 до a =b, где tgb=y/x:

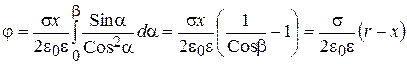(2.87)

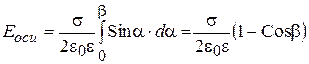(2.88)

В центре диска х=0, r = R, b = p/2, Cosb=0 и (2.87), (2.88) примут вид:

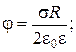
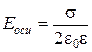(2.89)

Если диск является проводящим (металлическим), то из-за взаимного отталкивания заряды распределены по поверхности не равномерно. В центре диска поверхностная плотность меньше чем на краях. Распределение поверхностной плотности можно оценить по формуле [10]:

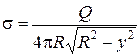(2.90)

В центре диска (у=0) поверхностная плотность заряда s в четыре раза меньше, чем в случае равномерного распределения заряда по площади диска (S = pR²). Край диска соответствует значению y = R. Знаменатель в (2.90) обращается в нуль, а напряженность на краю стремится к бесконечности. В реальных электродных системах, когда толщина диска является конечной величиной, радиус кривизны не является бесконечно малым, и напряженность остается конечной. Расчет напряженности на краю диска проводится методом конформных отображений, который рассматривается далее в этой главе. Собственная емкость проводящего диска равна:

С = 8e₀eК (2.91)