Непрерывный вейвлет-анализ.

Основныеприложения непрерывного вейвлет-анализа: локализация и классификация особых точек сигнала, частотно-временной анализ нестационарных сигналов. Глобальная задача сжатия информации – сократить этот объем при сохранении приемлемого качества. В этом существенную роль и играет вейвлет-анализ.

Фактически, для того, чтобы функция ψ(t) могла принадлежать к классу вейвлетов, необходимо выполнение двух условий:

1. График функции ψ(t) должен быть локален и осцилировать вокруг нуля в окрестности некоторой точки на оси времени, и резко убывать при

t → ± ∞; при этом ее среднее значение (т.е. интеграл по времени) равно нулю:

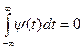; (14.1)

2. Норма функции (ее энергия) должна быть конечной:

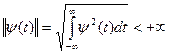(14.2)

В радиотехнике непрерывный вейвлет-анализ часто осуществляется с помощью трех функций (рис. 14.1). Это вейвлеты Добеши, Морле и перевернутое «сомбреро».

Возмем произвольный непериодический сигнал неизменной амплитуды u(t) (ЛЧМ-сигнал) и в упрощенной форме произведем его вейвлет-анализ при помощи вейвлета «сомбреро» (рис. 14.1), причем переменную х назовем временем. Результатом вейвлет-анализа этого сигнала будет функция

W_u(x,a), которая зависит уже от двух переменных – от времени х и некоторого масштаба осциляции а.

Непрерывное вейвлет-преобразование сигнала u(t) определяется с помощью произвольной функции вейвлета ψ(х) и выглядит таким образом

W_u(x,a) = 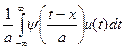(14.3)

В нижней части рисунка изображен график исследуемого сигнала, в верхней в виде ломанной линии – распределение значений W_u(x,a) (по горизонтали – переменная х, по вертикали – ось а. Прямоугольниками изображены графики вейвлета ψ_x,a при разных значениях х и а (х₁, а₁ и х₂, а₂). Выделенные участки графика исходного сигнала u(t) поточечно умножаются на значения оказавшихся над ними столбиков, потом все это суммируется. Абсолютная величина суммы определяет, где будет координата (х,а) на верхней картинке ( на рисунке они выделены жирными точками). Это делается для всех пар (х,а). Параметр х является аналогом координаты времени t ( т.е. характеризует смещение сигнала во времени) а параметр а – аналогом периода осциляции ( т.е. обратной частоте а = 1/f). Значит вейвлет-преобразование W_u(x,a) содержит информацию о частотных и временн′ых или пространственных свойствах сигнала одновременно. Это и позволяет изучить сложный сигнал более детально, чем с помощью преобразования Фурье. Для сравнения слева на верхней части условно приведена спектральная плотность S(f)анализируемого сигнала. Наглядность этого представления совершенно не сравнима наглядностью вейвлет-преобразования. На рис. 14.2 видна наклонная кривая, по которой можно определить начальную частоту, конечную частоту и характер изменения локальной частоты колебаний.