Шумоподобные сигналы

В настоящее время в теоретической радиотехнике, теории электросвязи, теории информации и прикладной математике усиленно разрабатываются методы синтеза сигналов с заданными (оптимальными) автокорреляционными и спектральными свойствами. Если рассматривать последовательности из n импульсовпрямоугольной формы, которые в соответствии с номером позиции М могут принимать значения ±1, то простым перебором можно найти такие последовательности, для которых

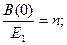Е = nЕ₁, (13.10)

где В(0) – автокорреляционная функция; Е – энергия всего сигнала, Е₁ – энергия одного элемента.

В иностранной технической и научной литературе такие сигналы принято называть шумоподобными сигналами (ШПС), сигналами без несущей, сигналами с рассеянным спектром или секвентными сигналами. В основе структуры секвентного сигнала и его анализа лежит понятие секвента. По определению секвента равна числу изменений знака несинусоидальных функций за единицу времени. Обычно под секвентными сигналами понимается последовательность импульсов одинаковой формы и единичной амплитуды, но различного знака. Структура секвентных сигналов хорошо приспособлена для современных цифровых систем связи, и особенно это касается мобильных систем. Секвентные сигналы, во-первых, позволяют уплотнить перегруженный частотный диапазон, во-вторых, обеспечивают скрытность передачи информации или абонентских переговоров.

Секвентные сигналы можно назвать почти ортогональными. По своим характеристикам и свойствам почти ортогональные сигналы приближаются к белому шуму, поэтому в отечественной литературе их часто называют шумоподобными или широкополосными сигналами – их корреляционные функции и спектры плотности мощности близки к аналогичным характеристикам квазибелого шума. Шумоподобные сигналы относятся к классу сложных сигналов, база которых Вс = 2F_cT_c >> 1.

Наиболее распространенным примером технической реализации шумоподобных сигналов могут служить сформированные определенным образом псевдослучайные последовательности прямоугольных радиоимпульсов, в частности, при манипуляции несущего колебания двоичными кодами. База таких сигналов определяется числом модулирующих импульсов в исходной последовательности. При этом наиболее успешно развиваются цифровые методы передачи и обработки сигналов на основе дискретных ортогональных последовательностей в виде функций Баркера, линейных рекурентных М-последовательностей (последовательности Голда, Лежандра и пр.), Радемахера, Уолша и др.