Непрерывный код может быть только избыточным.

Из непрерывных кодов наиболее широкое распростра­нение получили рекуррентные коды, иначе называемые цепными ко­дами, и их разновидность – сверточные коды [2].

Кодовые символы кодовой последовательности сверточного кода формируются в результате свертки исходной кодовой последовательности с импульсной реакцией кодера сверточного кода.

Избыточные коды могут быть систематическими и несистематическими.

Избыточный блочный код называется систематическим, если в его КК можно выделить информационную и проверочную части.

Информационную часть КК систематического блочного кода формирует отрезок (блок) символов первичной кодовой последовательности, поступающей с выхода ОА, а символы проверочной части формируют из символов информационной части путем их линейных комбинаций, например, сложением по модулю 2.

Примером систематического блочного кода является код (15, 10) систем телеуправления-телесигнализации (ТУ-ТС) в некоторых системах связи.

Избыточный блочный код называется несистематическим, если в его КК нельзя выделить информационную и проверочную части.

Примером несистематического блочного кода является рассмотренный семиэлементный телеграфный код МТК № 3.

Непрерывные коды могут быть систематическими и несистематическими.

Непрерывный код называется систематическим, если изего кодовой последовательности можно выделить кодовые символы первичной передаваемой кодовой последовательности. В противном случае непрерывный код называется несистематическим.

Примером несистематического непрерывного кода является широко используемый несистематический сверточный код НСК-1/2.

Контрольные вопросы

1. Какие коды называются непрерывными?

2. Какие коды называются блочными?

3. Какой код называется примитивным?

4. Может ли непрерывный код быть примитивным и почему?

5. Может ли неравномерный код быть примитивным и почему?

6. Что такое разрешенные и запрещенные кодовые комбинации?

7. Какие коды называются систематическими?

8. Какие коды называются несистематическими?

9. В чем отличие систематических непрерывных от систематических блочных кодов?

10. Что такое взвешенные и невзвешенные коды?

Основные задачи теории кодирования

И пути их решения

При выборе кода в общем случае приходится решать две основ­ные задачи теории кодирования.

Первая задача теории кодирования заключается в отыскании кода, обеспечивающего максимальную скорость передачи символов источника сообщения v_ис по каналу связи с заданной скоростью передачи элементов сигнала v_с.

Если символы источника сообщений закодировать кодовыми комбинациями одинаковой длины n (равномерный код), то

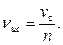
и увеличение v_ис может быть достигнуто за счет уменьшения n.

Если символы источника неравновероятны, то можно осуществить более экономное неравномерное кодирование, присваивая наи­более вероятным символам сообщения КК меньшей длины, а наименее вероятным – более длинные КК. Тогда у неравномерного кода средняя длина кодовой комбинации:

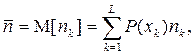
в общем случае меньше n и ИС может выдавать символы со средней скоростью

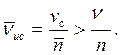
Таким образом, решение первой задачитеории кодирования заключается в отыскании неравномерного кода, имеющего минимальную среднюю длину кодовой комбинации .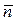

Вторая задача теории кодирования связана с выбором кода, обеспечивающего наименьшую вероятность ошибки при передаче символа источника сообщения х_k.

Для решения второй задачи теории кодирования надо использовать избыточное кодирование. В этом случае в результате ошибки в одном или нескольких разрядах принятой КК может сформироваться как разрешенная, так и запрещенная КК. Если сформируется разрешенная КК, то переданный символ будет принят неправильно, а если запрещенная КК, то ошибка может быть обнаружена или исправлена.

При декодировании с обнаружением ошибок потерянные символы частично или полностью можно восстановить путем их повторной передачи. Потеря информации здесь возможна из-за появления необнаруженных ошибок, т.е. ошибок, приводящих к формированию разрешенных кодовых комбинаций. Поэтому для уменьшения вероятности ошибки надо выбирать код, имеющий большой процент запрещенных кодовых комбинаций, что возможно только при увеличении числа избыточных символов, а значит, при увеличении длины КК.

Таким образом, длярешения второй задачи теории кодирования надо увеличивать длину КК, что противоречит решению первой задачи теории кодирования.

Из изложенного следует, что решения этих задач противоречат одна другой.

Выходом из этого противоречия может быть укрупнение алфавита ИС. Для укрупнения алфавита ИС осуществляют простое преобразование, заключающееся в том, что каждую группу из q символов исходного алфавита {х_k} объемом L, последовательно формируемых ИС, рассматривают как один символ укрупненного алфавита q_i. Множество укрупненных символов {q_i} образует новый алфавит объемом L^q, называемый укрупненным алфавитом. Из изложенного следует, что при укрупнении символов алфавита источника сообщений резко возрастают трудности, связанные с практической реализацией кодера и декодера.

Поэтому практически в настоящее время это противоречие разрешают следующим образом:

- символы алфавита передаваемого сообщения кодируют в ОАпримитивным равномернымили неравномерным кодом, формируя на выходе ОА первичную кодовую последовательность минимальной длины (т.е. решают первую задачу теории кодирования);

- полученную первичную кодовую последовательность кодируют помехоустойчивым кодом с минимально необходимой избыточностью, обеспечивающей требуемую помехоустойчивость передачи сообщения, и максимально возможной длиной информационной части КК (т.е. решают вторую и первую задачи теории кодирования).

В электросвязи для кодирования сообщений широко применяют примитивные равномерные международные телеграфные коды МТК № 2 и МТК № 5 (табл. 1.2 и 1.3) [11]. Из неравномерных кодов наибольшее распространение в системах связи получили неравномерные коды Шеннона-Фано и Хаффмана. Неравномерный код Хаффмана является оптимальным в том смысле, что нельзя построить код с меньшей средней длиной кодовой комбинации [11].

Из помехоустойчивых кодов наибольшее распространение в электросвязи получили циклические и сверточные коды. Циклические коды относятся к классу блочных равномерных систематических кодов, а сверточные коды – к классу непрерывных кодов. Из циклических кодов наибольшее распространение получили коды БЧХ (Боуза-Чоудхари-Хоквингема), Голея, Рида-Соломона, а из сверточных кодов – несистематический сверточный код НСК-1/2 [11].

Помехоустойчивые блочные коды могут задаваться таблично, линейными операциями над символами информационной части КК, а также в матричной и полиномиальной форме. В настоящее время преимущественно используется полиномиальная форма.

Для понимания принципов построения помехоустойчивых блочных кодов рассмотрим табличное задание помехоустойчивого кода и задание помехоустойчивого кода линейными операциями над символами информационной части КК.

Табличное задание помехоустойчивых кодов было первым способом задания помехоустойчивого кода и реализация его кажется весьма простой:

- составляется таблица из L символов алфавита ИС и устанавливается их соответствие разрешен­ным КК;

- в память кодирующего устройства (кодера) записываются разре­шенные КК выбранного кода и правило, по которому каждому из L символов алфавита источника сообщений сопоставляют одну из разрешен­ных КК (данное правило известно при построении декодера);

- получив от источника определенный символ сообщения, ко­дер отыскивает соответствующую ему КК и отсылает ее в канал связи;

- декодер, приняв КК, искаженную помехами в канале связи, сравни­вает ее со всеми L разрешенными КК и отыскивает ту из них, кодовое расстояние от которой до принятой КК меньше, и отправляет соответствующий ей символ алфавита получателю сообще­ния.

Табличный способ задания помехоустойчивых кодов прост для малых n, а для достаточно эффективных кодов (n >> 1) – технически невозможен.

По табличному способу задания, например, построен избыточный семиэлементный международный телеграфный код МТК № 3 (табл. 1.2). В нем разрешенными являются только КК, в которых три кодовые символа «1». Количество возможных кодовых комбинаций этого кода M = 2⁷ = 128, а разрешенных только

.

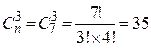В этой связи одним из основных направлений развития теории помехо­устойчивого кодирования является отыскание таких классов кодов, для которых кодирование и декодирование осуществляются не табличным методом, а с помощью регулярных правил, определяемых алгебраиче­ской структурой кодовых комбинаций.

Задание блочных равномерных систематических кодов (n, k) линейными операциями над символами информационной части КК (n – длина кодовой комбинации; k – длина информационной части кодовой комбинации; (n – k) = r – длина проверочной части кодовой комбинации).

В качестве примера рассмотрим построение блочного равномерного систематического кода (7, 3):

1. Обозначим символы КК блочного систематического кода (7, 3) следующим образом:

α₁, α₂, α₃│α₄, α₅, α₆, α₇.

Символы α₁, α₂, α₃ составляют информационную часть, а α₄, α₅, α₆, α₇ – проверочную часть КК систематического кода.

2. Информационная часть КК кода (7, 3) имеет длину k = 3. Определим, какие возможны комбинации трехразрядных кодовых символов:

000, 001, 010, 011, 100, 101, 110, 111.

3. Для определения значений символов проверочной части КК блочного систематического кода введем следующее правило линейных операций над сим­волами информацион­ной части:

α₄ = α₁ + α₂; α₅ = α₁ + α₃; α₆ = α₂ + α₃; α₇ = α₁ + α₂ + α₃,

где суммирование осуществляется по модулю 2.[3]

Например, если информационная часть КК имеет вид 010, то получим:

α₄ = 0 + 1 = 1; α₅ = 0 + 0 = 0; α₆ = 1 + 0 = 1; α₇ = 0 + 1 + 0 = 1,

т.е. проверочная часть КК имеет вид 1011, тогда КК блочного равномерного систематического кода имеет вид 010 1011.

Рассмотренный способ построения помехоустойчивых кодов удобнее табличного, но он основан на множестве возможных субъективных правил формирования символов проверочной части, что усложняет его техническую реализацию для достаточно эффективных кодов (n >> 1).

Матричный способ задания кода (n, k) был следующим шагом к совершенствованию способов задания блочных равномерных систематических кодов. Сущность данного способа:

- задается образующая матрица размерности n × k (n – количество столбцов матрицы; k – количество строк матрицы);

- информационную часть КК представляют в виде матрицы-строки длины k;

- перемножают матрицу-строку и образующую матрицу и получают матрицу-строку, соответствующую КК блочного равномерного систематического кода.

Недостатком данного способа является громоздкость расчетов при n >> 1.

В настоящее время применяют полиномиальный способ задания кода(n, k).При этом способе задания кода КК блочного равномерного систематического кода получается путем алгебраических действий (сложение и умножение по модулю 2) над образующим полиномом и полиномом, соответствующим информационной части КК [11].

Сверточный код НСК-k/n задаютправилом формирования n символов выходной помехоустойчивой кодовой последовательности из k поступивших на вход кодера символов первичной кодовой последовательности [11]. Например, для кода НСК-1/2 – это правило формирования двухсимволов выходной помехоустойчивой кодовой последовательности на один символ первичной кодовой последовательности, поступившей на вход кодера.

Сравнение сверточных и блочных кодов показало, что характеристики помехоустойчивости (исправляющей способности) сверточных кодов лучше аналогичных характеристик блочных кодов той же длины.

Сверточные коды нашли применение в системах спутниковой связи, в системах подвижной радиосвязи и в мобильной связи.

Контрольные вопросы

1. Первая задача теории кодирования и пути ее решения.

2. Вторая задача теории кодирования и пути ее решения.

3. В чем противоречивость решения первой и второй задач теории кодирования?

4. Что такое разрешенная и запрещенная кодовые комбинации?

5. Пути разрешения противоречий при решении первой и второй задач теории кодирования.

6. Способы задания помехоустойчивых кодов.

7. Достоинства и недостатки табличного способа задания кода.

8. Как определить КК блочного равномерного систематического кода по заданной образующей матрице?

9. Как определить КК блочного равномерного систематического кода по заданному образующему полиному?

10.Чему равны результаты суммирования по модулю 2 различных двоичных кодовых символов?

11.Чему равны результаты умножения по модулю 2 различных двоичных кодовых символов?